Capítulo 3 Estadística inferencial
La estadísticas descriptiva es la rama de las estadística que tiene como objetivo describir y resumir un conjunto de datos de la mejor manera posible, es decir, con la menor pérdida de información posible. Con la estadística descriptiva no hay incertidumbre, porque describimos solo el grupo de observaciones en las que decidimos trabajar y no se intenta generalizar las características observadas o estudiar un grupo más grande a partir de un conjunto de datos limitado.
Por otro lado, La estadística inferencial es la rama de la estadística que utiliza una muestra aleatoria de datos tomados de una población para hacer inferencias, es decir, sacar conclusiones sobre la población de interés. En otras palabras, la información de la muestra se utiliza para hacer generalizaciones sobre el parámetro de interés en la población.
Las dos herramientas más importantes utilizadas en estadística inferencial son los test de hipótesis y los intervalos de confianza.
Ver caso de bulos o noticias fake
La estadística inferencial proporciona las herramientas que necesitamos para responder a este tipo de preguntas, y dado que este tipo de preguntas y es una pieza fundamental de lo que podriamos denominar lenguaje científico. Sin embargo, la inferencia estadística se basa en la teoría de la probabilidad. Aquí no vamos a hablar de probabilidad pero, ya que la teoría de la probabilidad sustenta gran parte de las estadísticas, vale la pena cubrir algunos de los conceptos básicos.
3.1 Diferencia entre probabilidad y estadística
Probabilidad y estadística son dos disciplinas que están estrechamente relacionadas pero no son idénticas. La teoría de la probabilidad es “la doctrina de las posibilidades”. Es una rama de las matemáticas que estiaud con qué frecuencia ocurrirán diferentes tipos de eventos. Por ejemplo, todas estas preguntas son cosas que puede responder usando la teoría de la probabilidad:
- ¿Cuáles son las posibilidades de que una moneda corriente salga cara 10 veces seguidas?
- Si tiro dos dados de seis caras, ¿qué probabilidad hay de que saque dos seises?
- ¿Qué posibilidades hay de que cinco cartas extraídas de una baraja perfectamente mezclada sean corazones?
- ¿Cuáles son las posibilidades de que me toque la lotería?
Todas estas preguntas tienen algo en común. En cada caso, la “verdad” se conoce de antemano, y cada pregunta se relaciona con “qué tipo de eventos” sucederán. En la primera pregunta, sabiendo que no se trata de una moneda trucada, hay un 50% de posibilidades de que cualquier lanzamiento de moneda individual salga cara. En la segunda pregunta, sabemos que la posibilidad de sacar un 6 en un solo dado es de 1 entre 6. En la tercera pregunta, conocemos también el número de cartas y que han sido barajadas perfectamente. En la cuarta pregunta, también se conocen las reglas específicas de cada juego (Euromillones, Primitiva, Loteria de Navidad, etc). El punto crítico es que las preguntas probabilísticas comienzan con un modelo conocido del mundo, y usamos ese modelo para hacer algunos cálculos. El modelo subyacente puede ser bastante simple. Por ejemplo, en el ejemplo del lanzamiento de una moneda, podemos escribir el modelo de esta manera:
\[ P(\mbox{caras}) = 0.5 \] que se puede leer como “la probabilidad de que salga cara es 0,5 sobre 1” (las probabilidades son solo números que van del 0 al 1). Utilizamos este modelo pero, no se sabe exactamente lo que va a pasar. Todo es posible. Tal vez salgan diez caras, como dice la pregunta, pero tal vez consiga tres caras. Dicho de otro modo, en la teoría de la probabilidad, el modelo es conocido, pero los datos no.
En cambio, las preguntas estadísticas funcionan al revés. En estadística, no conocemos la “verdad” pero tenemos algunos datos, y es a partir de los datos que queremos aprender la “verdad”. Las preguntas estadísticas tienden a parecerse más a estas:
- Si alguien lanza una moneda 10 veces y obtiene 10 caras, ¿me están haciendo trampas?
- Si cinco cartas de la parte superior de la baraja son todos corazones, ¿qué probabilidad hay de que la baraja se haya barajado?
- Si un político gana n veces seguidas a la lotería, ¿qué probabilidades hay de que nos ensté engañando?
Esta vez, lo único que tenemos son datos. Se sabe lo que ha sucedido y se infiere si todo ha sucedido de un modo normal o si hay alguna regla que no se ha respetado. Los datos que tenemos se ven así:
Cara Cara Cara Cara Cara Cara Cara Cara Cara Caray lo que tratamos de averiguar es si debemos confiar en que esto sea “verdad”. Si la moneda es una moneda común, entonces el modelo que debo adoptar es uno que diga que la probabilidad de que salga cara es 0.5; es decir, \(P(\mbox{caras}) = 0.5\). Si la moneda está trucada, entonces debería concluir que la probabilidad de que salga cara es no 0.5, que escribiríamos como \(P(\mbox{caras})\neq0.5\). En otras palabras, el problema de la inferencia estadística es averiguar cuál de estos dos modelos de la realidad es el correcto. Así pues, la pregunta estadística no es la misma que la pregunta de probabilidad, pero están profundamente conectadas entre sí. Debido a esto, una buena introducción a la teoría estadística comenzará con una discusión sobre qué es la probabilidad y cómo funciona.
3.2 Probabilidad frecuentista vs Bayesiana
3.2.1 Enfoque frecuentista
El enfoque predominante para el estudio de la probabilidad en estadística, se conoce como punto de vista frecuentista, y define la probabilidad como una frecuencia a largo plazo. Lanzando una moneda que tiene \(P(caras) = 0.5\) podría suceder lo siguiente:
Cruz,Cara,Cara,Cara,Cara,Cruz,Cruz,Cara,Cara,Cara,Cara,Cruz,Cara,Cara,Cruz,Cruz,Cruz,Cruz,Cruz,CaraEn este caso, 11 de estas 20 monedas (55%) salieron cara. Ahora supongamos que he estado llevando un recuento continuo del número de caras (que llamaré \(N_{caras}\)) que he visto, en los primeros \(N\) volteos, y calculo la proporción de caras \(N_{caras}/N\) cada vez. Esto es lo que obtendría (¡literalmente lancé monedas para producir esto!):
| Lanzamientos | Caras | Proporción |
|---|---|---|
| 1 | 0 | 0.00 |
| 2 | 1 | 0.50 |
| 3 | 2 | 0.67 |
| 4 | 3 | 0.75 |
| 5 | 4 | 0.80 |
| 6 | 4 | 0.67 |
| 7 | 4 | 0.57 |
| 8 | 5 | 0.63 |
| 9 | 6 | 0.67 |
| 10 | 7 | 0.70 |
| 11 | 8 | 0.73 |
| 12 | 8 | 0.67 |
| 13 | 9 | 0.69 |
| 14 | 10 | 0.71 |
| 15 | 10 | 0.67 |
| 16 | 10 | 0.63 |
| 17 | 10 | 0.59 |
| 18 | 10 | 0.56 |
| 19 | 10 | 0.53 |
| 20 | 11 | 0.55 |
Al comienzo de la secuencia, la proporción de caras fluctúa mucho, comenzando en .00 y subiendo hasta .80. Después de un cierto número de lanzamientos, da la impresión de que se la proporción disminuye un poco, y que cada vez más valores se acercan bastante a la respuesta que sabemo que es la “correcta” (.50). Esta es la definición frecuentista de probabilidad.
Lanza una moneda común una y otra vez, y a medida que \(N\) crece (se acerca al infinito, denotado \(N\rightarrow\infty\)), la proporción de caras se acercará al 50%.
Simulando con un ordenador es posible lanzar una moneda virtual 1000 veces para ver lo que sucede con la proporción \(N_{caras}/N\) a medida que aumenta \(N\). Los resultados se muestran en la Figura 3.1. La proporción de caras observadas finalmente deja de fluctuar y se estabiliza; cuando lo hace, el número en el que finalmente se asienta es la verdadera probabilidad de que salga cara.
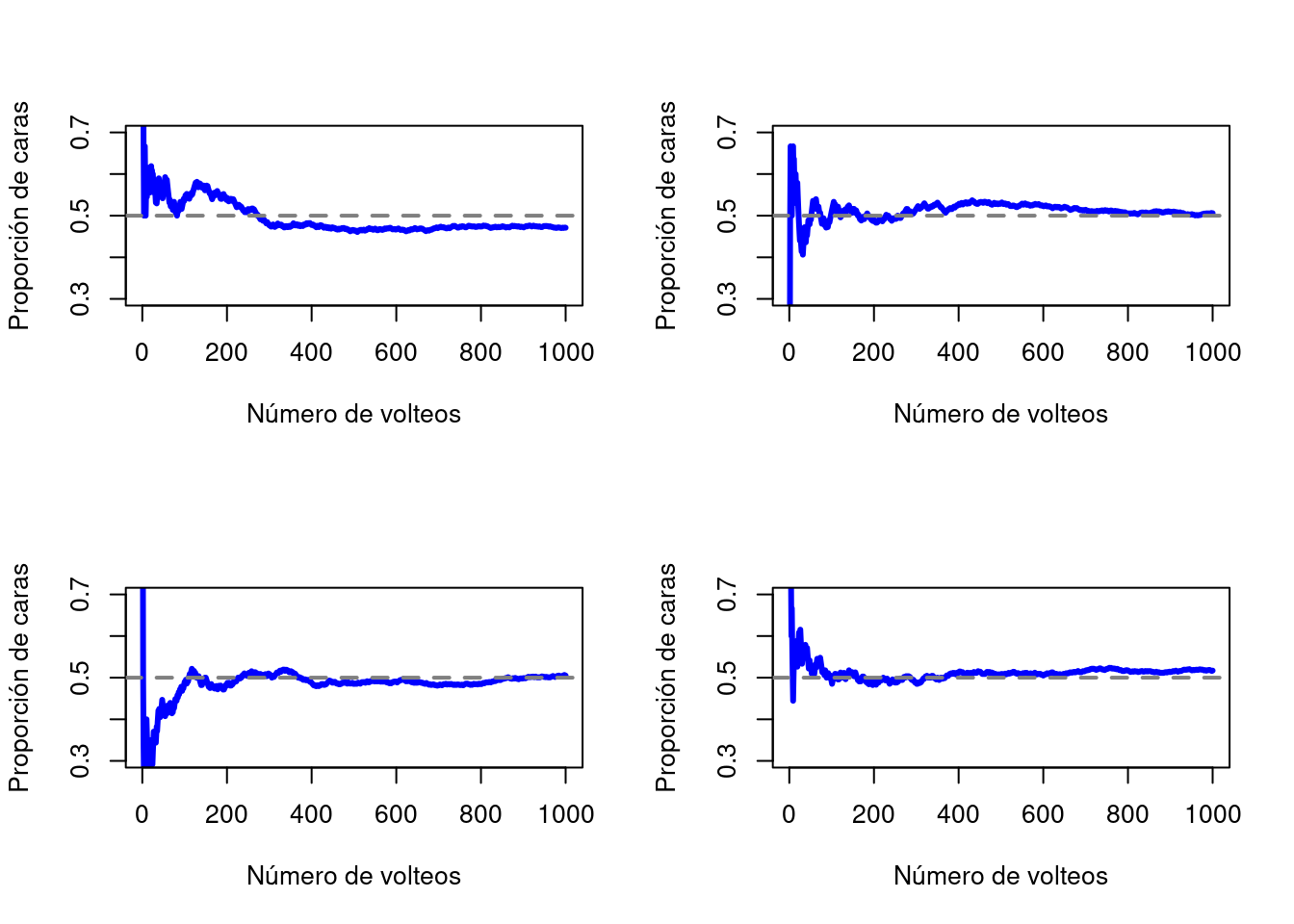
Figura 3.1: Una ilustración de cómo funciona la probabilidad frecuentista. Si lanzamos una moneda una y otra vez, la proporción de caras que ha visto finalmente se estabiliza y converge a la probabilidad real de 0.5. Cada panel muestra cuatro experimentos simulados diferentes: en cada caso, simulamos que lanzamos una moneda 1000 veces y seguimos la pista de la proporción de lanzamientos que fueron caras a medida que avanzamos. Aunque ninguna de estas secuencias en realidad terminó con un valor exacto de .5, si hubiéramos extendido el experimento para un número infinito de lanzamientos de monedas, lo hubieran hecho.
La definición frecuentista de probabilidad resulta bastante interesante puesto que: 1. Es objetiva. La probabilidad de un evento está necesariamente basada en el la realidad. Los enunciados de probabilidad pueden tener sentido si se refieren a (una secuencia de) eventos que ocurren en el universo físico. 2. Es inequívoca. Dos personas cualesquiera que observen el desarrollo de la misma secuencia de eventos, tratando de calcular la probabilidad de un evento, inevitablemente deben llegar a la misma respuesta.
Sin embargo, también hay que tener ciertas precauciones ya que: 1. Las secuencias infinitas no existen en el mundo físico. Por ejemplo, si se toma una moneda y se comienza a lanzar al suelo infinitas veces, cada vez que aterriza, impacta contra el suelo. Cada impacto desgasta un poco la moneda; eventualmente, la moneda quedará modificada y ya no volverá a ser la misma. 2. La definición frecuentista tiene un alcance limitado. Por ejemplo, si un meteorólogo aparece en la televisión y dice: “la probabilidad de que llueva en Adelaida el 2 de noviembre de 2022 es del 60%”, no está claro cómo definir esto en términos frecuentistas. Solo hay una ciudad de Adelaide, y solo habrà un 2 de noviembre de 2022. No hay una secuencia infinita de eventos aquí, solo una vez. La probabilidad frecuentista no contempla hacer enunciados de probabilidad sobre un solo evento. Desde la perspectiva frecuentista, mañana lloverá o no; no hay “probabilidad” que se adhiera a un solo evento no repetible.
3.2.2 Enfoque Bayesiano
El enfoque bayesiana de la probabilidad a menudo se denomina visión subjetivista, y es una visión minoritaria entre los estadísticos, pero que ha ido ganando terreno de manera constante durante las últimas décadas. La forma más común de pensar sobre la probabilidad subjetiva es definir la probabilidad de un evento como el grado de creencia que alguien inteligente y racional asigna a la probabilidad de ese evento. Según esto, las probabilidades no existen en el mundo, sino en los pensamientos y suposiciones de las personas. Sin embargo, para que este enfoque funcione, necesitamos alguna forma de operacionalizar “grado de creencia”. Supongamos que creo que hay un 60% de probabilidad de que llueva mañana. Si alguien me ofrece una apuesta: si mañana llueve, gano 5 euros, pero si no llueve, pierdo 5 euros. Claramente, desde mi perspectiva, esta es una apuesta bastante buena. Por otro lado, si creo que la probabilidad de lluvia es solo del 40%, entonces es una mala apuesta. Por lo tanto, podemos operacionalizar la noción de una “probabilidad subjetiva” en términos de las apuestas que estoy dispuesto a aceptar.
¿Cuáles son las ventajas y desventajas del enfoque bayesiano? La principal ventaja es que te permite asignar probabilidades a cualquier evento. No es necesario que se limite a los eventos que se pueden repetir. La principal desventaja es que no podemos ser puramente objetivos: especificar una probabilidad requiere que especifiquemos una entidad que tenga el grado de creencia relevante. Esta entidad puede ser un humano, un extraterrestre, un robot o incluso un estadístico, pero tiene que haber un agente inteligente que crea en las cosas. Para mucha gente esto es incómodo: parece hacer que la probabilidad sea arbitraria. Si bien el enfoque bayesiano requiere que el agente en cuestión sea racional (es decir, obedezca las reglas de probabilidad), sí permite que todos tengan sus propias creencias; Puedo creer que la moneda es común y tú no tienes que hacerlo, aunque ambos seamos racionales. La visión frecuentista no permite que dos observadores atribuyan diferentes probabilidades al mismo evento: cuando eso sucede, al menos uno de ellos debe estar equivocado. La visión bayesiana no evita que esto ocurra. Dos observadores con conocimientos previos diferentes pueden tener legítimamente creencias diferentes sobre el mismo evento. En resumen, donde la visión frecuentista a veces se considera demasiado estrecha (prohíbe muchas cosas a las que queremos asignar probabilidades), la visión bayesiana a veces se piensa que es demasiado amplia (permite demasiadas diferencias entre observadores).
3.3 Introducción a las distribuciones de probabilidad
Una distribución de probabilidad es una función que describe la probabilidad de obtener los posibles valores que puede asumir una variable aleatoria. En otras palabras, los valores de la variable varían según la distribución de probabilidad subyacente.
Supongamos que seleccionamos una muestra aleatoria de personas y medimos la altura de los sujetos. A medida que vamos midiendo las alturas, podemos crear una distribución de alturas. Este tipo de distribución es útil cuando necesita saber qué resultados son más probables, la dispersión de los valores potenciales y la probabilidad de resultados diferentes. Por lo tanto se puede utilizar distribuciones de probabilidad para realizar inferencias.
Ejemplo a partir de la película “El sargento de hierro” de Clint Eastwood.
Supongamos que el profesor solo tiene 5 jerseis (\(X_1\), \(X_2\), \(X_3\), \(X_4\) y \(X_5\). Cada prenda (es decir, cada \(X\)) sería un evento elemental. La característica clave de los eventos elementales es que cada vez que hacemos una observación (por ejemplo, cada vez que me pongo un jersey), el resultado será uno y solo uno de estos eventos. De manera similar, el conjunto de todos los eventos posibles se denomina espacio muestral.
Definido el espacio muestral, que se construye a partir de muchos posibles eventos elementales (jerseys), lo que queremos hacer es asignar una probabilidad de uno de estos eventos elementales. Para un evento \(X\), la probabilidad de ese evento \(P(X)\) es un número que se encuentra entre 0 y 1. Cuanto mayor sea el valor de \(P(X)\), es más probable que ocurra el evento. Entonces, por ejemplo, si \(P(X)=0\), significa que el evento \(X\) es imposible (es decir, nunca uso ese jersey). Por otro lado, si \(P(X)=1\) significa que el evento \(X\) seguramente ocurrirá (es decir, siempre uso ese jersey). Todos los demas valores, entre 0 y 1, significarían que unas veces uso un jersey y otras veces otros. Por ejemplo, si \(P(X)=0.5\) significa que uso ese jersey la mitad del tiempo.
Las probabilidades de los todos los eventos elementales deben sumar 1. Esto se conoce como la ley de la probabilidad total. Si se satisfacen estos requisitos, entonces lo que tenemos es una distribución de probabilidad. Por ejemplo, este es un ejemplo de distribución de probabilidad
| Jersey | Azul | Gris | Naranja | Amarillo | Marrón |
|---|---|---|---|---|---|
| Etiqueta | \(X_1\) | \(X_2\) | \(X_3\) | \(X_4\) | \(X_5\) |
| Probabildad | \(P(X_1) = .5\) | \(P(X_2) = .3\) | \(P(X_3) = .1\) | \(P(X_4) = 0\) | \(P(X_5) = .1\) |
Cada uno de los eventos tiene una probabilidad que se encuentra entre 0 y 1, y si sumamos la probabilidad de todos los eventos, suman 1. Impresionante. Incluso podemos dibujar un bonito gráfico de barras para visualizar esta distribución, como se muestra en la Figura ??.
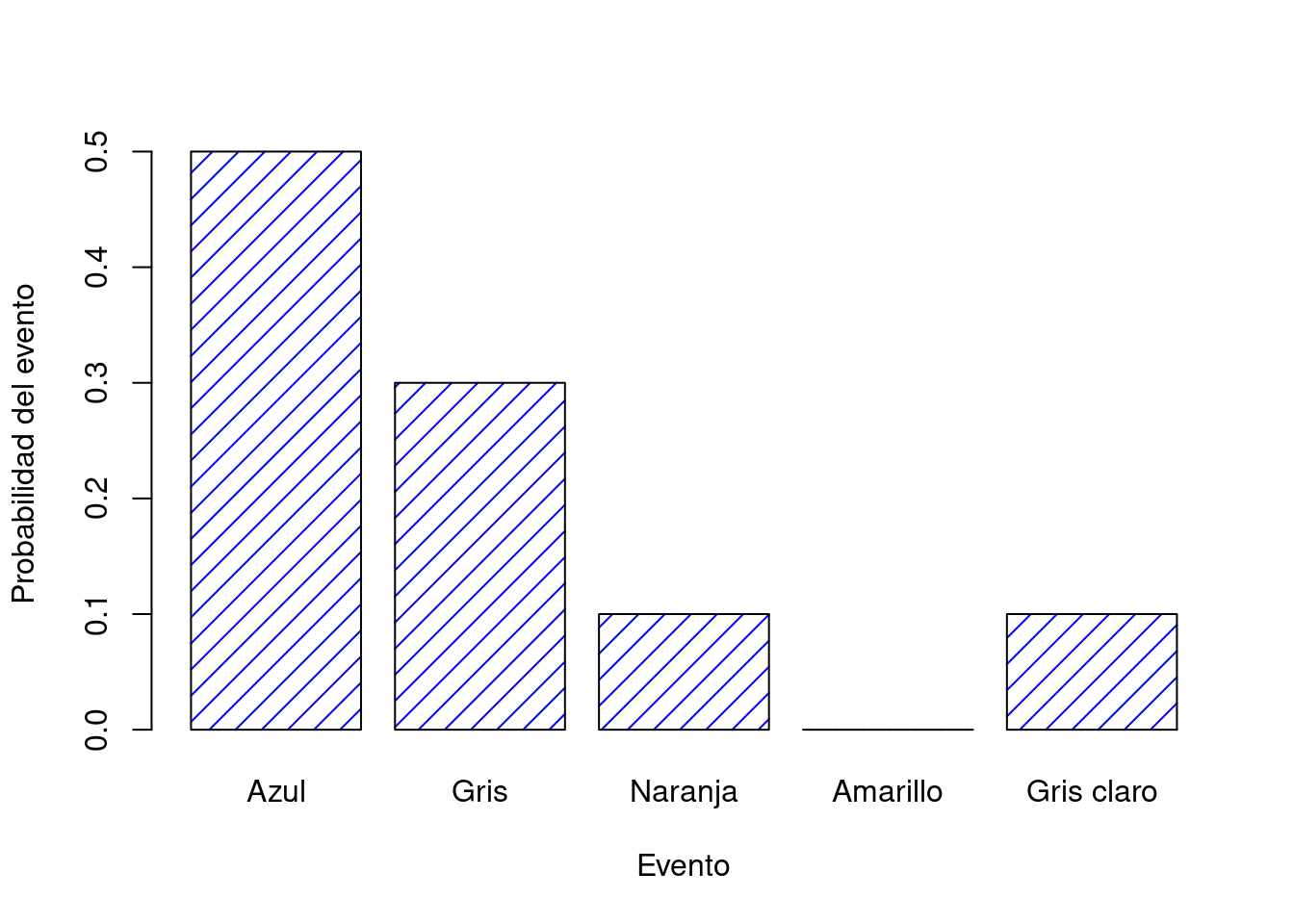
Figura 3.2: Representación visual de la distribución de probabilidad de jerseys del profesor. Hay cinco eventos elementales, correspondientes a los cinco jerseys. Cada evento tiene alguna probabilidad de ocurrir: esta probabilidad es un número entre 0 y 1. La suma de estas probabilidades es 1.
Cabe ser señalado es que la teoría de la probabilidad permite hablar de eventos elementales y también de eventos no elementales. En el ejemplo de los jerseys, es perfectamente legítimo referirse a la probabilidad de que vista un color claro. En términos matemáticos, definimos el evento “jersey de color claro” \(E\) para que corresponda al conjunto de eventos elementales \((X_1, X_2, X_3)\). Si ocurre alguno de estos eventos elementales, también se dice que ha ocurrido \(E\). Habiendo decidido escribir la definición de \(E\) de esta manera, es bastante sencillo establecer cuál es la probabilidad \(P(E)\): simplemente sumamos todo. En este caso particular \[ P(E) = P(X_1) + P(X_2) + P(X_3) \] y, dado que las probabilidades de los jerseys amarillo, naranja y gris claro, respectivamente, son .1, 0 y .1, la probabilidad de que use un jersey de color claro es igual a .2.
A partir de estos principios tan simples es posible construir algunas herramientas matemáticas extremadamente poderosas. En la Tabla 3.1 aparecen algunas de las otras reglas que satisfacen las probabilidades.
| Expresión | Notación | NANA | Formula |
|---|---|---|---|
| No \(A\) | \(P(\neg A)\) | = | \(1-P(A)\) |
| \(A\) o \(B\) | \(P(A \cup B)\) | = | \(P(A) + P(B) - P(A \cap B)\) |
| \(A\) y \(B\) | \(P(A \cap B)\) | = | \(P(A|B) P(B)\) |
Las distribuciones de probabilidad varían enormemente. Sin embargo, no todas son igualmente importantes. Las más utilizadas serían: la distribución binomial, la distribución normal, la distribución \(t\), la distribución \(\ chi^2\) (“chi-cuadrado”) y la distribución distribución de \(F\). Aquí prestaremos especial atención a la binomial y a la normal.
3.3.1 La distribución binomial
La teoría de la probabilidad se originó en el intento de describir cómo funcionan los juegos de azar, por lo que parece apropiado que nuestra discusión sobre la distribución binomial incluya una discusión sobre el lanzamiento de dados y monedas. Imaginemos un “experimento” simple: en un cubilete hay 20 dados idénticos de seis caras. En una cara de cada dado hay una imagen de un bufón (joker) y las otras cinco caras están todas en blanco. Si lanzamos los 20 dados, ¿cuál es la probabilidad de que obtenga exactamente 4 jokers? Suponiendo que los dados no estén trucados, sabemos que la probabilidad de que se obtenga un joker es de 1 en 6; Para decir esto de otra manera, la probabilidad de joker para un solo dado es aproximadamente \(.167\).
Si \(N\) es el número de tiradas de dados en nuestro experimento; que a menudo se denomina parámetro de tamaño de nuestra distribución binomial. Mientras que \(\theta\) es la probabilidad de que un solo dado produzca un joker, una cantidad que generalmente se llama probabilidad de éxito del binomio. Finalmente, \(X\) serán resultados de nuestro experimento, es decir, el número de jokers obtenido al tirar los dados. Dado que el valor real de \(X\) se debe al azar, nos referimos a él como variable aleatoria. La cantidad que queremos calcular es la probabilidad de que \(X=4\) dado que sabemos que \(\theta=.167\) y \(N=20\). La “forma” general de lo que me interesa calcular podría escribirse como
\[ P(X \ | \ \theta, N) \] y estamos interesados en el caso especial donde \(X=4\), \(\theta=.167\) y \(N=20\). Si quiero decir que \(X\) se genera aleatoriamente a partir de una distribución binomial con los parámetros \(\theta\) y \(N\), la notación que usaría es la siguiente: \[ X \sim \mbox{Binomial}(\theta, N) \] La distribución binomial tiene el aspecto que muestar en la Figura 3.3 y traza las probabilidades binomiales para todos los valores posibles de \(X\). Si se lanzan los dados, desde \(X=0\) (sin jokers) hasta \(X=20\) (todos los jokers). Esto es básicamente un gráfico de barras, y no es diferente del gráfico de “probabilidad de jerseys”de la Figura 3.2. En el eje horizontal tenemos todos los eventos posibles y en el eje vertical podemos leer la probabilidad de cada uno de esos eventos. Entonces, la probabilidad de sacar 4 jokers de 20 veces es de aproximadamente 0.20. En otras palabras, esperaría que eso sucediera aproximadamente el 20% de las veces que se lancen los dados.
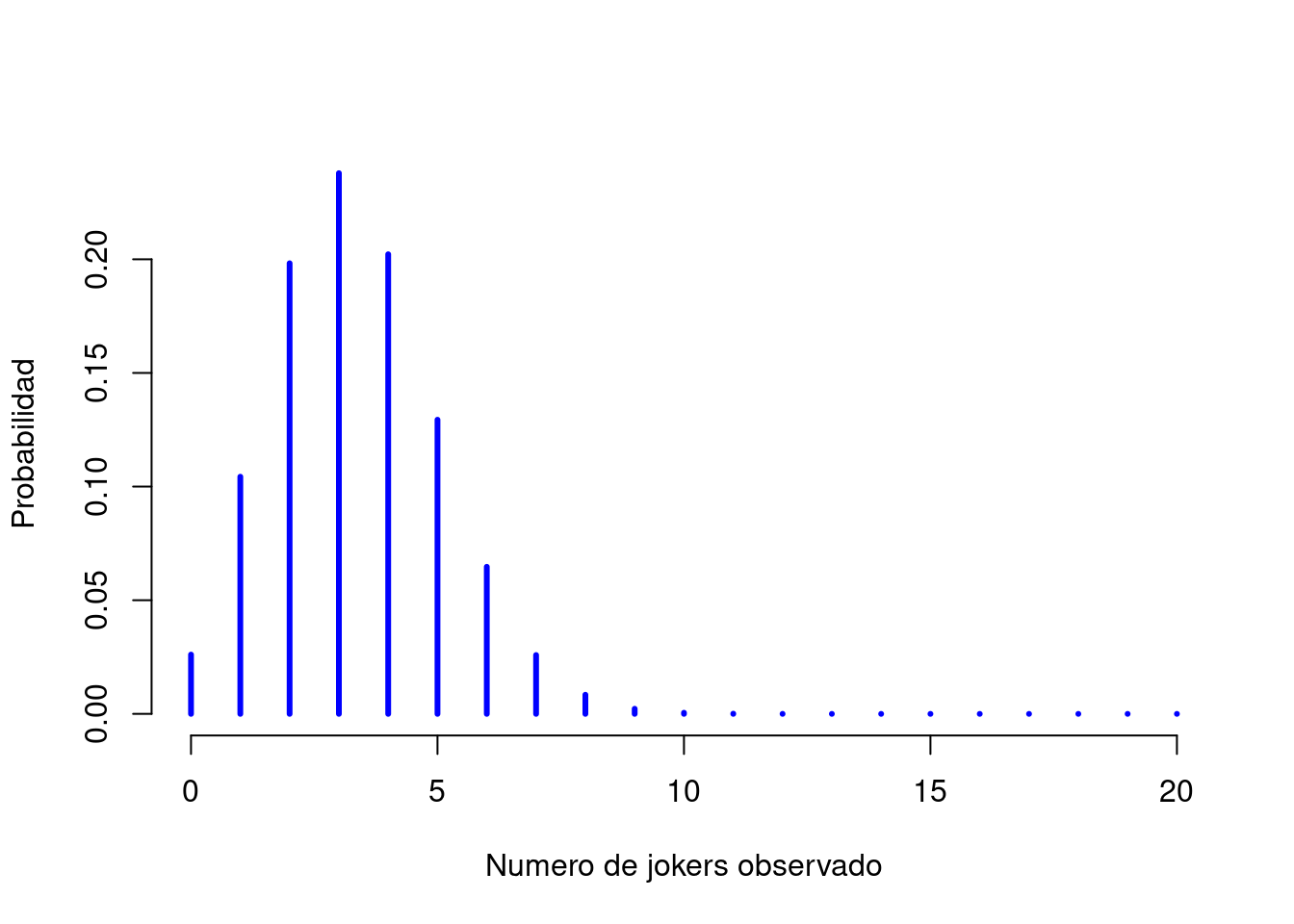
Figura 3.3: La distribución binomial con parámetro de tamaño de \(N=20\) y una probabilidad de éxito subyacente de \(theta=1/6\). Cada barra vertical representa la probabilidad de un resultado específico (es decir, un valor posible de \(X\)). Debido a que esta es una distribución de probabilidad, cada una de las probabilidades debe ser un número entre 0 y 1, y las alturas de las barras también deben sumar 1.
Como se ha visto en la tabla ??, R tiene una función llamada dbinom () que calcula probabilidades binomiales. Los principales argumentos de la función son:
x. Éste es un número o vector, que especifica los resultados cuya probabilidad se está tratando de calcular.size. Este es un número que le dice a R el tamaño del experimento.prob. Ésta es la probabilidad de éxito de cualquier ensayo del experimento.
Entonces, para calcular la probabilidad de obtener x = 4 jokers, a partir de un experimento de size = 20 ensayos, en el que la probabilidad de obtener un joker en cualquier ensayo es prob = 1/6, el comando que usaríamos es:
## [1] 0.2022036Para ver cómo cambia la distribución binomial cuando modificamos los valores de \(\theta\) y \(N\), cambiemos los dados por monedas. De este modo, la probabilidad de éxito ahora es \(\theta=1/2\). Suponiendo que se lanzara la moneda \(N=20\) veces. Es decir que estamos cambiando la probabilidad de éxito, pero manteniendo el tamaño del experimento. Como muestra la Figura 3.4, el efecto principal de esto es cambiar toda la distribución. ¿Y si lanzamos una moneda \(N=100\) veces? Bueno, en ese caso, se obtiene la distribución que aparece en la Figura 3.5. La distribución se mantiene aproximadamente en el medio, pero hay un poco más de variabilidad en los posibles resultados.
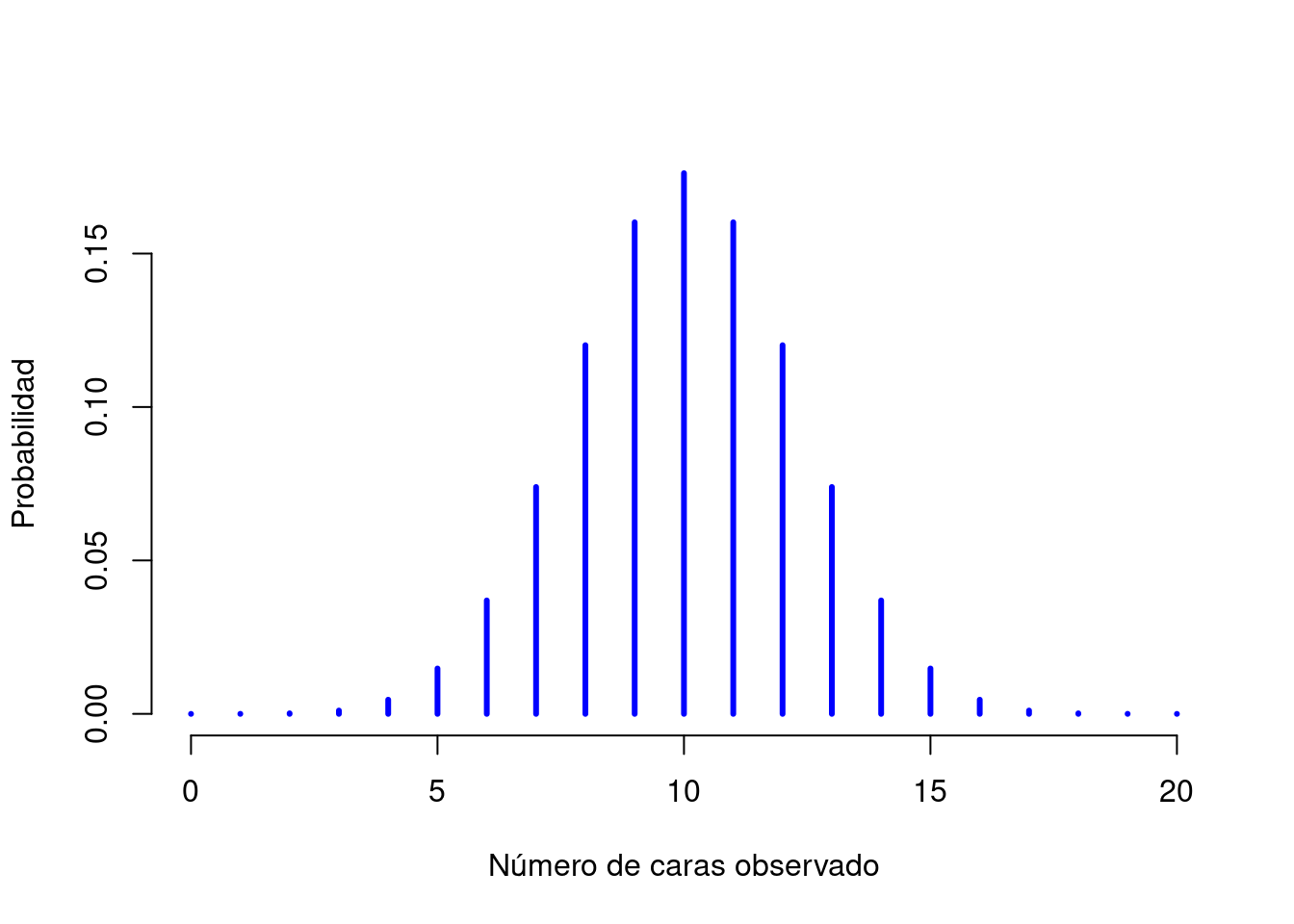
Figura 3.4: Dos distribuciones binomiales, que involucran un escenario en el que estoy lanzando una moneda, por lo que la probabilidad de éxito subyacente es \(theta=1/2\). Aquí asumimos que estoy lanzando la moneda \(N=20\) veces.
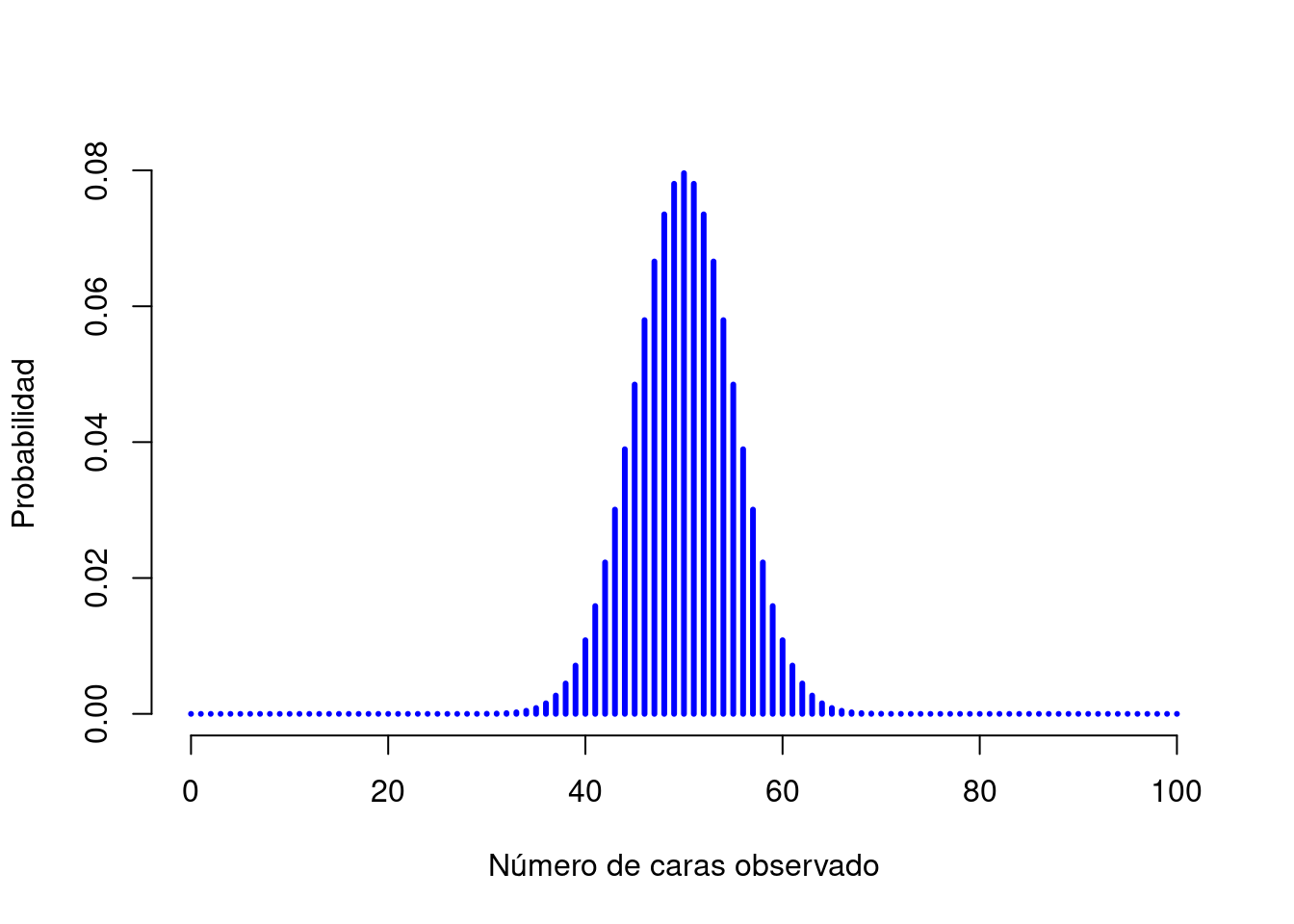
Figura 3.5: Dos distribuciones binomiales, que involucran un escenario en el que se lanza una moneda, por lo que la probabilidad de éxito subyacente es \(theta=1/2\). Aquí asumimos que la moneda se lanza \(N=100\) veces.
La fórmula de la distribución binomial que calcula R es la siguiente: \(P(X | \theta, N) = \displaystyle\frac{N!}{X! (N-X)!} \theta^X (1-\theta)^{N-X}\)
3.3.2 La distribución normal
La fórmula de la distribución normal que calcula R es la siguiente: \(p(X | \mu, \sigma) = \displaystyle\frac{1}{\sqrt{2\pi}\sigma} \exp \left( -\frac{(X - \mu)^2}{2\sigma^2} \right)\)
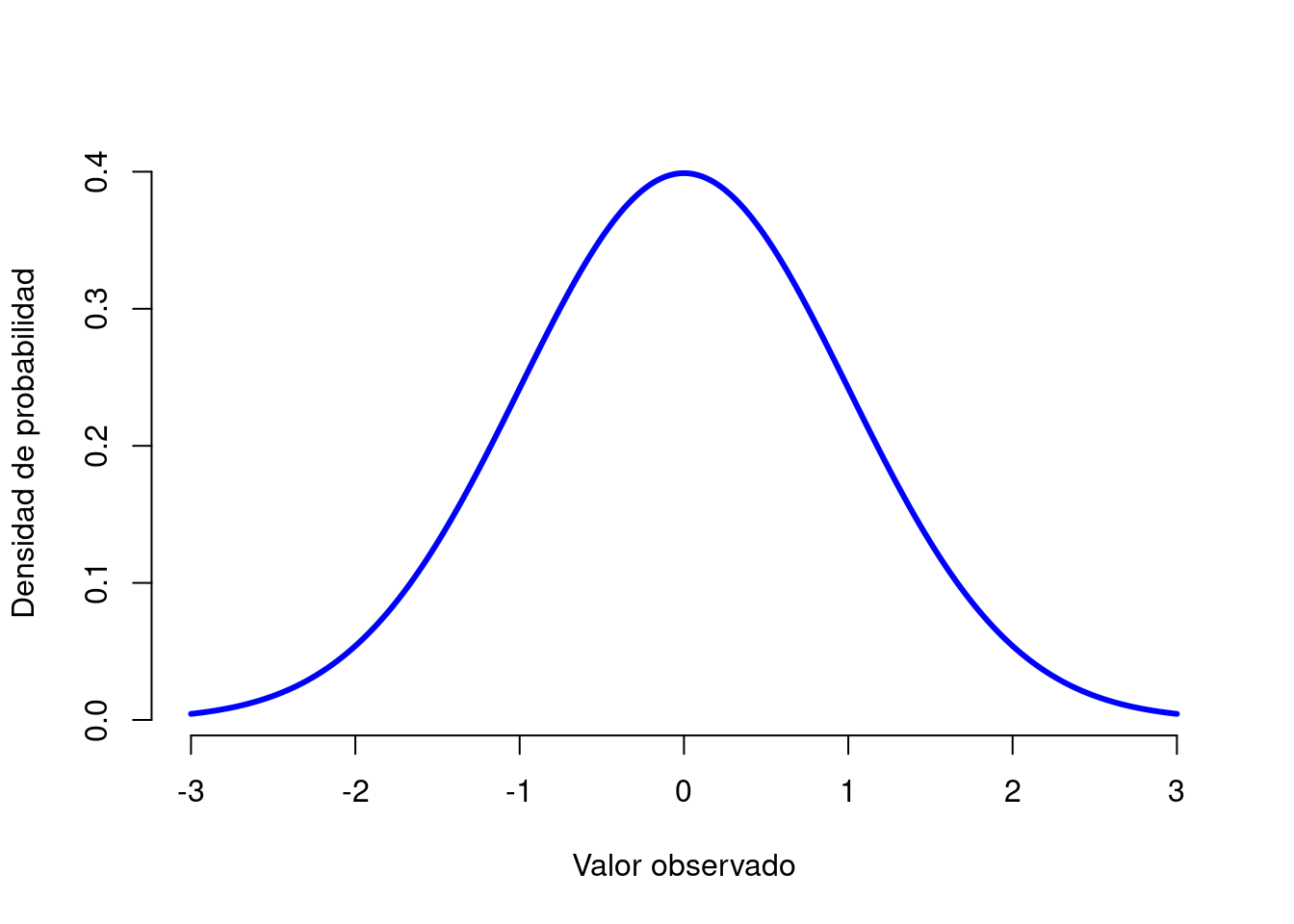
Figura 3.6: {La distribución normal con media \(mu=0\) y desviación estándar \(sigma = 1\). El eje \(x\) corresponde al valor de alguna variable, y el eje \(y\) nos dice algo sobre la probabilidad de que observemos ese valor. Sin embargo, observe que el eje \(y\) está etiquetado como “Densidad de probabilidad” y no como “Probabilidad”. Existe una característica sutil y algo frustrante de las distribuciones continuas que hace que el eje \(y\) se comporte un poco extraño: la altura de la curva aquí no es en realidad la probabilidad de observar un valor particular de \(x\). Por otro lado, es cierto que las alturas de la curva indican qué valores de \(x\) son más probables.
La distribución normal, que también se conoce como “de campana” o una “distribución gaussiana” es la distribución más utilizada. Una distribución normal se describe usando dos parámetros, la media de la distribución \(\mu\) y la desviación estándar de la distribución \(\sigma\). La notación que a veces usamos para decir que una variable \(X\) se distribuye normalmente es la siguiente:
\[ X \sim \mbox{Normal}(\mu,\sigma) \]
3.3.3 Funciones de R para distribuciones de probabilidad
R tiene varias funciones para trabajar con cada distribución de probabilidad. Hay un nombre de raíz, por ejemplo, el nombre de raíz para la distribución normal es norm. Esta raíz tiene como prefijo una de las letras:
ppara “probabilidad”, la función de distribución acumulativa.qpara “cuantil”, el inverso de la función de distribución acumulativa.dpara “densidad”, la función de densidad.rpara “aleatorio”, una variable aleatoria que tiene la distribución especificada.
Las cuatro versiones de la cada función requieren que especifiquen los argumentos size yprob. Sin embargo, difieren en términos de cuál es el otro argumento y cuál es el resultado:
- La forma
drequiere un resultado particularx, y el devuelve la probabilidad de obtener exactamente ese resultado. - La forma
pcalcula la probabilidad acumulada. Se le da un cuantil particularq, y se le dice la probabilidad de obtener un resultado menor o igual queq. - La forma
qcalcula los cuantiles de la distribución. Se especifica un valor de probabilidadpy devuelve el percentil correspondiente. Es decir, el valor de la variable para el que existe una probabilidadpde obtener un resultado menor que ese valor. - La forma
res un generador de números aleatorios: específicamente, generanresultados aleatorios de la distribución.
Para la distribución normal, estas funciones son pnorm, qnorm, dnorm y rnorm, mientras que para la distribución binomial, estas funciones son pbinom, qbinom, dbinom y rbinom.
Para una distribución continua (como la normal), las funciones más útiles para resolver problemas que involucran cálculos de probabilidad son las funciones p y q, porque la densidad por la función d solo se puede usar para calcular probabilidades a través de integrales.
Para una distribución discreta (como la binomial), la función d calcula la densidad, Que en este caso es una probabilidad
\(f(x) = P(X = x)\)
y por lo tanto es útil para calcular probabilidades.
R tiene funciones para manejar muchas distribuciones de probabilidad. La siguiente tabla proporciona los nombres de las funciones para cada distribución y un enlace a la documentación en línea que es la referencia autorizada sobre cómo se utilizan las funciones. Pero no lea la documentación en línea todavía. Primero, pruebe los ejemplos de las secciones que siguen a la tabla.
| Distribution | p | q | d | r |
|---|---|---|---|---|
| Beta | pbeta | qbeta | dbeta | rbeta |
| Binomial | pbinom | qbinom | dbinom | rbinom |
| Cauchy | pcauchy | qcauchy | dcauchy | rcauchy |
| Chi-Square | pchisq | qchisq | dchisq | rchisq |
| Exponential | pexp | qexp | dexp | rexp |
| F | pf | qf | df | rf |
| Gamma | pgamma | qgamma | dgamma | rgamma |
| Geometric | pgeom | qgeom | dgeom | rgeom |
| Hypergeometric | phyper | qhyper | dhyper | rhyper |
| Logistic | plogis | qlogis | dlogis | rlogis |
| Log Normal | plnorm | qlnorm | dlnorm | rlnorm |
| Negative Binomial | pnbinom | qnbinom | dnbinom | rnbinom |
| Normal | pnorm | qnorm | dnorm | rnorm |
| Poisson | ppois | qpois | dpois | rpois |
| Student t | pt | qt | dt | rt |
| Studentized Range | ptukey | qtukey | dtukey | rtukey |
| Uniform | punif | qunif | dunif | runif |
| Weibull | pweibull | qweibull | dweibull | rweibull |
| Wilcoxon Rank Sum Statistic | pwilcox | qwilcox | dwilcox | rwilcox |
| Wilcoxon Signed Rank Statistic | psignrank | qsignrank | dsignrank | rsignrank |
3.3.4 Ejemplos con la distribución Binomial
De nuevo, si lanzamos dados, y cada dado tiene una probabilidad de 1 en 6 de obtener jokers, supongamos, que queremos saber la probabilidad de sacar 4 o menos jockers. Podríamos usar la función dbinom () para calcular la probabilidad exacta de obtener 0 jokers, 1 joker, 2 jokers, 3 jokers y 4 jokers y luego sumarlas, pero hay una manera más rápida. En su lugar, se puede usar la función pbinom ():
## [1] 0.7687492En otras palabras, hay un 76,9% de posibilidades de que saque 4 jokers o menos. R dice que un valor de 4 es en realidad el percentil 76,9 de esta distribución binomial.
A continuación, consideremos la función qbinom (). Digamos que queremos calcular el percentil 75 de la distribución binomial. Siguiendo con el ejemplo de los dados:
## [1] 4Lo que la función qbinom () parece estar diciendo es que el percentil 75 de la distribución binomial es 4, aunque según en la función pbinom () se sabe que 4 es en realidad el percentil 76,9. La rareza aquí proviene del hecho de que nuestra distribución binomial realmente no tiene un percentil 75. Hay un 56,7% de posibilidades de sacar 3 jokers o menos (ver pbinom (3, 20, 1/6)) y un 76,9% de posibilidades de sacar 4 calaveras o menos. Entonces, en cierto sentido el percentil 75 debería estar “entre” 3 y 4 jockers. Pero aquí los decimales no tienen sentido. Este problema se puede manejar de diferentes maneras:
- Se puede informar un valor intermedio (o un valor interpolado) como 3.9,
- Se puede redondear a la baja (a 3) o hacia arriba (a 4).
La función qbinom () redondea hacia arriba si se solicita un percentil que en realidad no existe (como el 75 en este ejemplo), R encuentra el valor más pequeño para el cual el rango percentil es al menos lo que se pidió. En este caso, dado que el percentil 75 “verdadero” se encuentra entre 3 y 4 jokers, R redondea y devuelve un valor de 4. Esto solo es un problema para distribuciones discretas como la binomial.
Finalmente, tenemos el generador de números aleatorios (rbinom ()). Hay que especificar cuántas veces R debe “simular” el experimento usando el argumento n, y generará resultados aleatorios a partir de la distribución binomial. Entonces, por ejemplo, supongamos que se tuviera que repetir el experimento de lanzamiento de dados 100 veces. Podría hacer que R simule los resultados de estos experimentos usando el siguiente comando:
## [1] 3 1 4 5 3 4 1 2 4 3 3 5 6 6 6 6 3 4 1 3 3 4 3 3 2 2 3 5 3 4 4 5 3 6 4 6 3
## [38] 5 2 3 4 3 6 3 0 2 1 3 1 4 4 4 5 1 2 5 7 6 4 6 4 1 3 3 4 3 4 2 2 2 2 2 2 2
## [75] 2 2 3 3 6 4 3 4 2 5 4 2 3 3 6 8 2 2 4 5 2 2 2 5 1 4Como puede ver, estos números son más o menos los que se puede ver en la Figura @ref(fig: binomial1). La mayoría de las veces se obtienen entre 1 y 5 jokers.
3.3.5 Ejemplos con la distribución normal
Como ya se ha dicho, las funciones R para la distribución normal son dnorm (), pnorm (), qnorm () y rnorm (). Sin embargo, se comportan prácticamente de la misma manera que las funciones correspondientes para la distribución binomial, por lo que no hay mucho que deba saber. Únicamente, cabe mencionar, que los nombres de los argumentos para los parámetros son mean ysd.
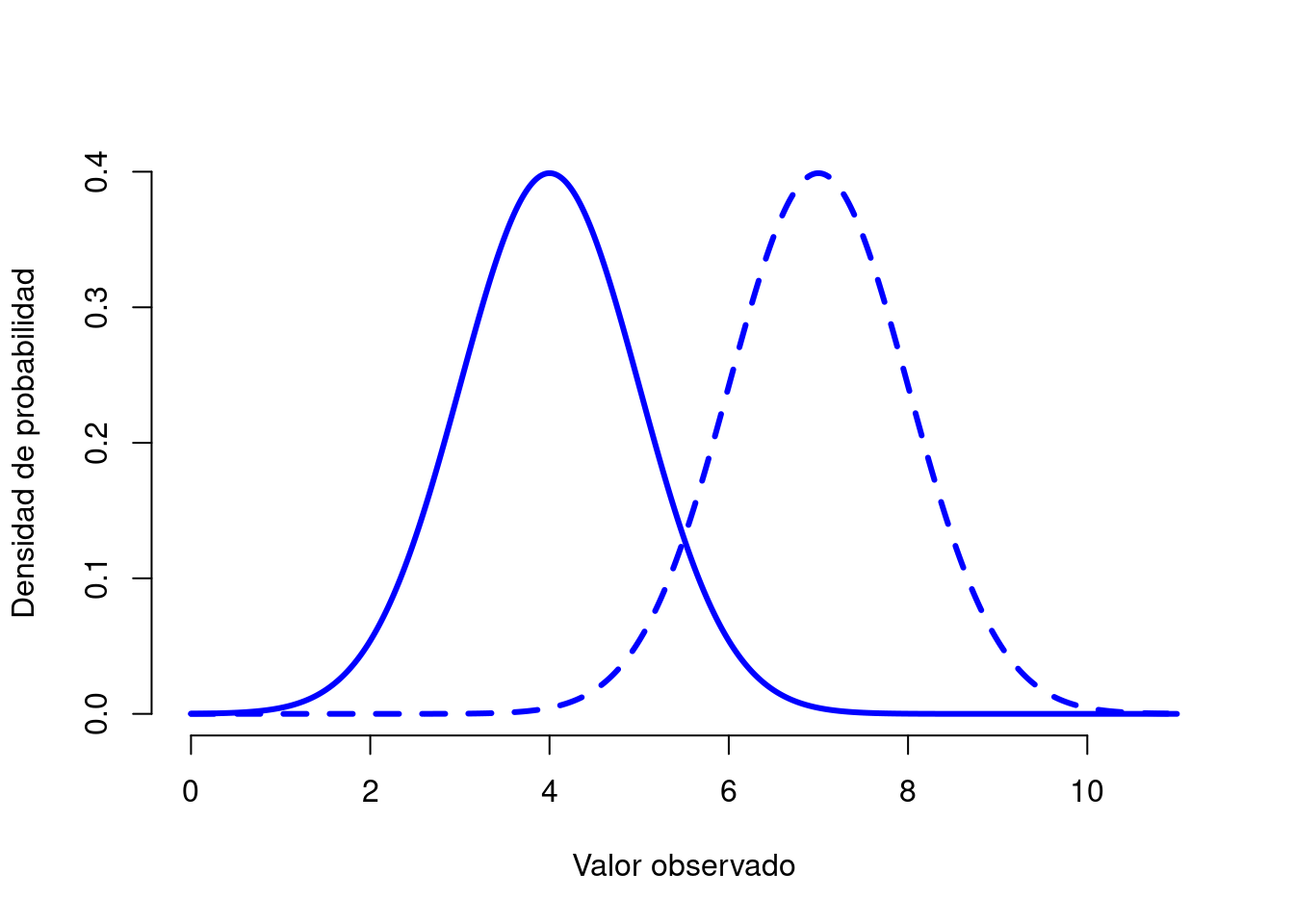
Figura 3.7: Ilustración de lo que sucede cuando cambia la media de una distribución normal. La línea continua representa una distribución normal con una media de \(mu=4\). La línea discontinua muestra una distribución normal con una media de \(mu=7\). En ambos casos, la desviación estándar es \(sigma=1\). Las dos distribuciones tienen la misma forma, pero la línea discontinua se desplaza hacia la derecha.
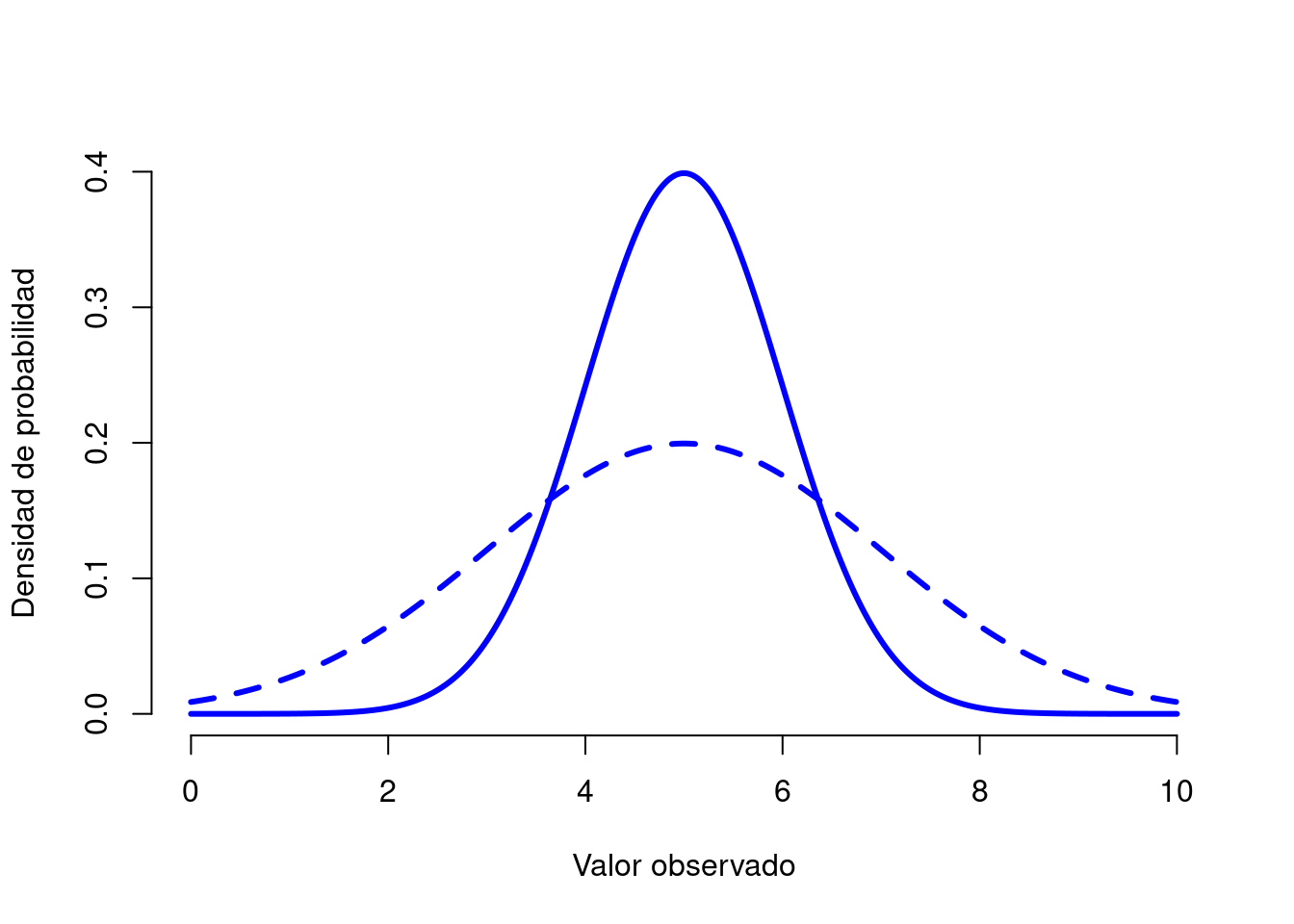
Figura 3.8: Ilustración de lo que sucede cuando cambia la desviación estándar de una distribución normal. Ambas distribuciones trazadas en esta figura tienen una media de \(mu=5\), pero tienen diferentes desviaciones estándar. La línea continua traza una distribución con desviación estándar \(sigma=1\), y la línea discontinua muestra una distribución con desviación estándar \(sigma=2\). Como consecuencia, ambas distribuciones están “centradas” en el mismo lugar, pero la línea discontinua es más ancha que la sólida.
En la Figura 3.6, se traza una distribución normal con media \(\mu=0\) y desviación estándar \(\sigma=1\). En vez de un histograma, la imagen de la distribución normal en la Figura 3.6 muestra una curva suave. Esta no es una elección arbitraria: la distribución normal es continua, mientras que la binomial es discreta. Las escalas continuas no tienen esta restricción. Por ejemplo, la temperatura de un día de primavera podría ser de 23 grados, 24 grados, 23,9 grados o cualquier punto intermedio, ya que la temperatura es una variable continua, por lo que una distribución normal podría ser muy apropiada para describir las temperaturas de primavera.
Mencionar el caso de las escalas Likert
La Figura 3.7 traza distribuciones normales que tienen diferentes medias, pero tienen la misma desviación estándar. Como era de esperar, todas estas distribuciones tienen el mismo “ancho”. La única diferencia entre ellos es que se han desplazado hacia la izquierda o hacia la derecha. En todos los demás aspectos, son idénticos. Por el contrario, si aumentamos la desviación estándar mientras mantenemos la media constante, el pico de la distribución permanece en el mismo lugar, pero la distribución se ensancha, como puede ver en la Figura 3.8. Sin embargo, cuando ampliamos la distribución, la altura del pico se reduce. Esto tiene que suceder: de la misma manera que las alturas de las barras que usamos para dibujar una distribución binomial discreta tienen que suma 1, el área total bajo la curva para la distribución normal debe ser igual a 1. No obstante, independientemente de cuál sea la media real y la desviación estándar, el 68,3% del área se encuentra dentro de 1 desviación estándar de la media. Del mismo modo, el 95,4% de la distribución se encuentra dentro de 2 desviaciones estándar de la media y el 99,7% de la distribución está dentro de 3 desviaciones estándar. Esta idea se ilustra en la Figura ??.
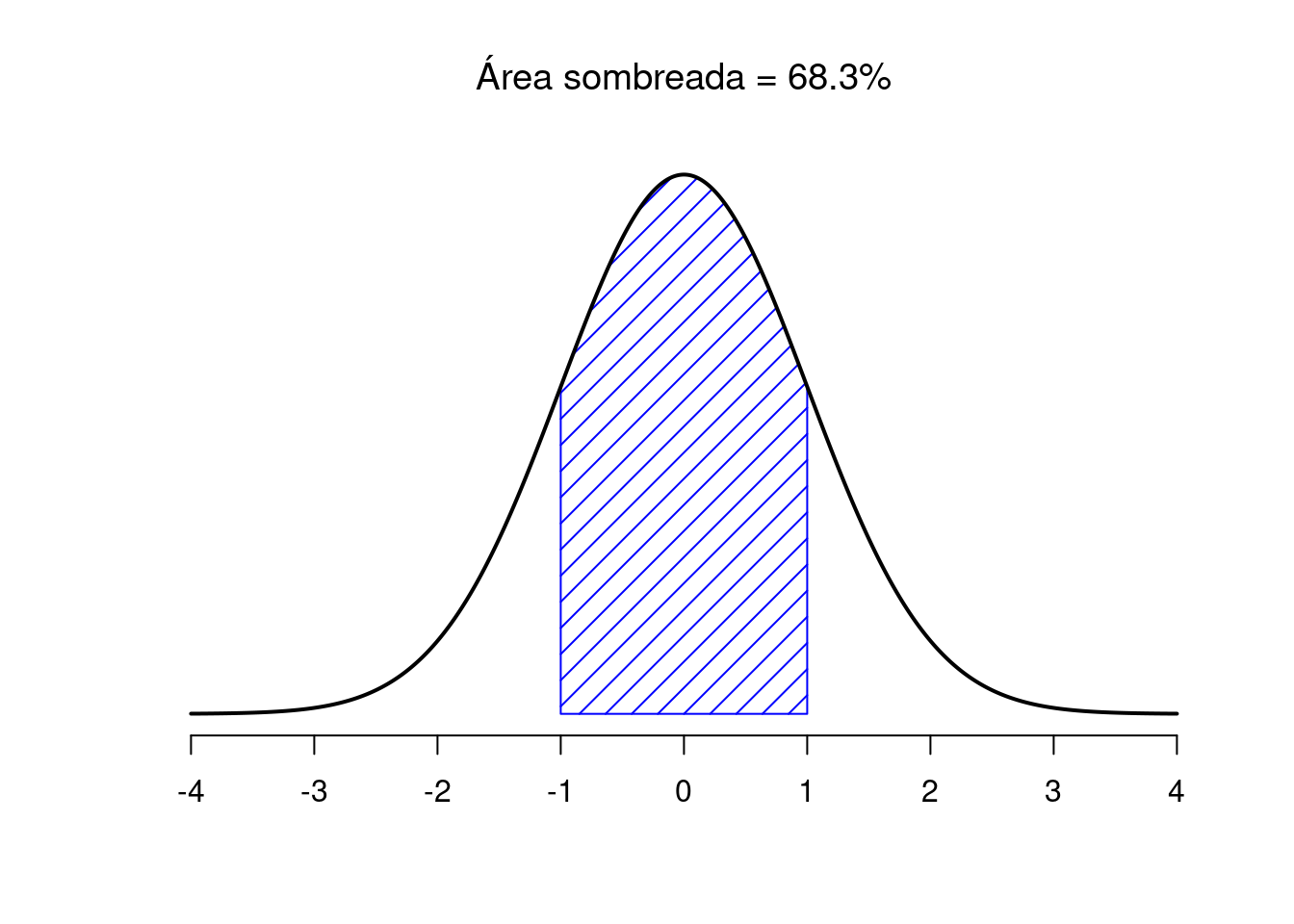
Figura 3.9: El área debajo de la curva indica la probabilidad de que una observación se encuentre dentro de un rango particular. Las líneas continuas trazan distribuciones normales con media \(mu=0\) y desviación estándar \(sigma=1\). Las áreas sombreadas ilustran “áreas bajo la curva” para dos casos importantes. Aquí podemos ver que hay un 68,3% de probabilidad de que una observación caiga dentro de una desviación estándar de la media.
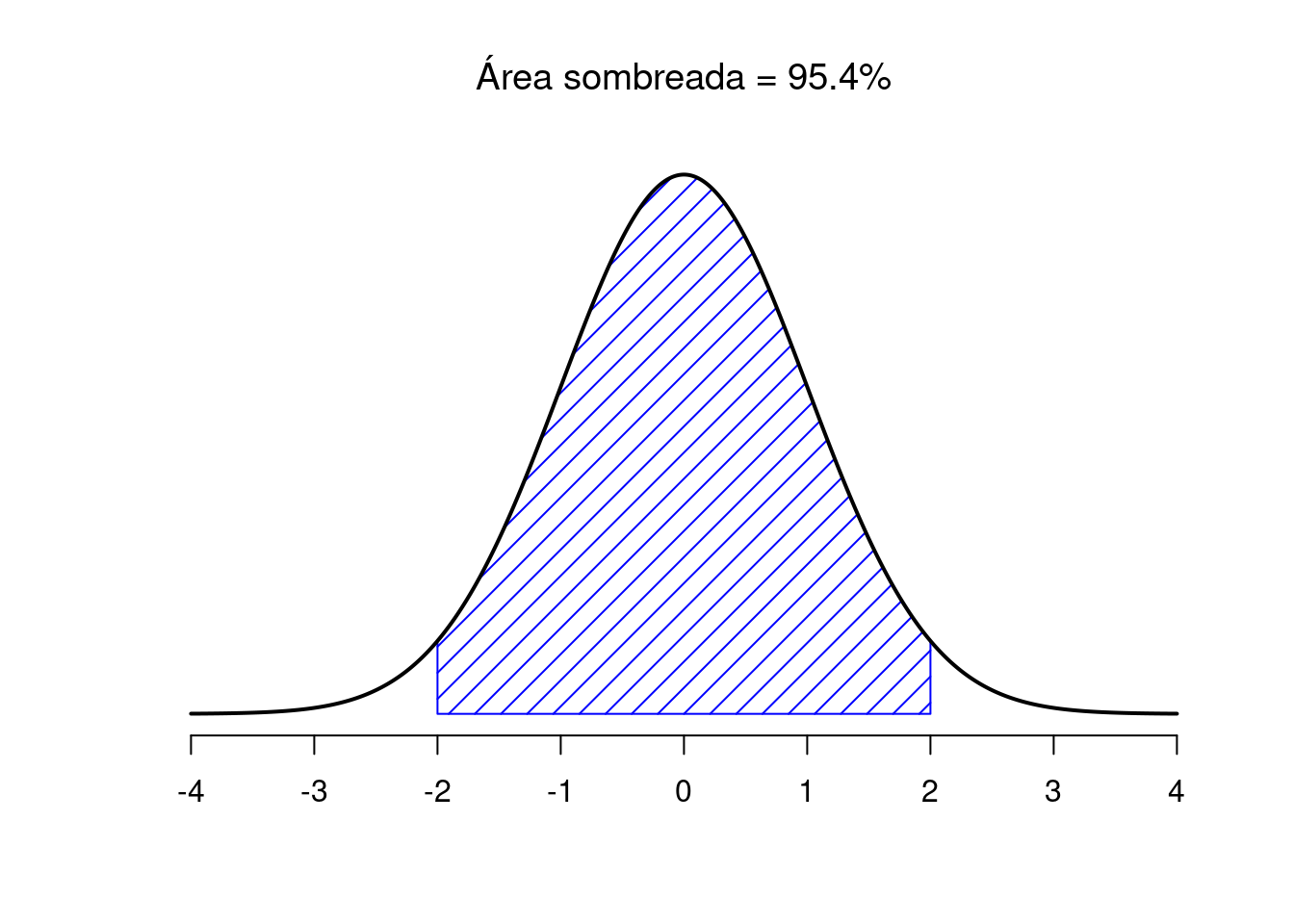
Figura 3.10: El área debajo de la curva indica la probabilidad de que una observación se encuentre dentro de un rango particular. Las líneas continuas trazan distribuciones normales con media \(mu = 0\) y desviación estándar \(sigma = 1\). Las áreas sombreadas ilustran “áreas bajo la curva” para dos casos importantes. Aquí vemos que hay un 95,4% de probabilidad de que una observación caiga dentro de dos desviaciones estándar de la media.
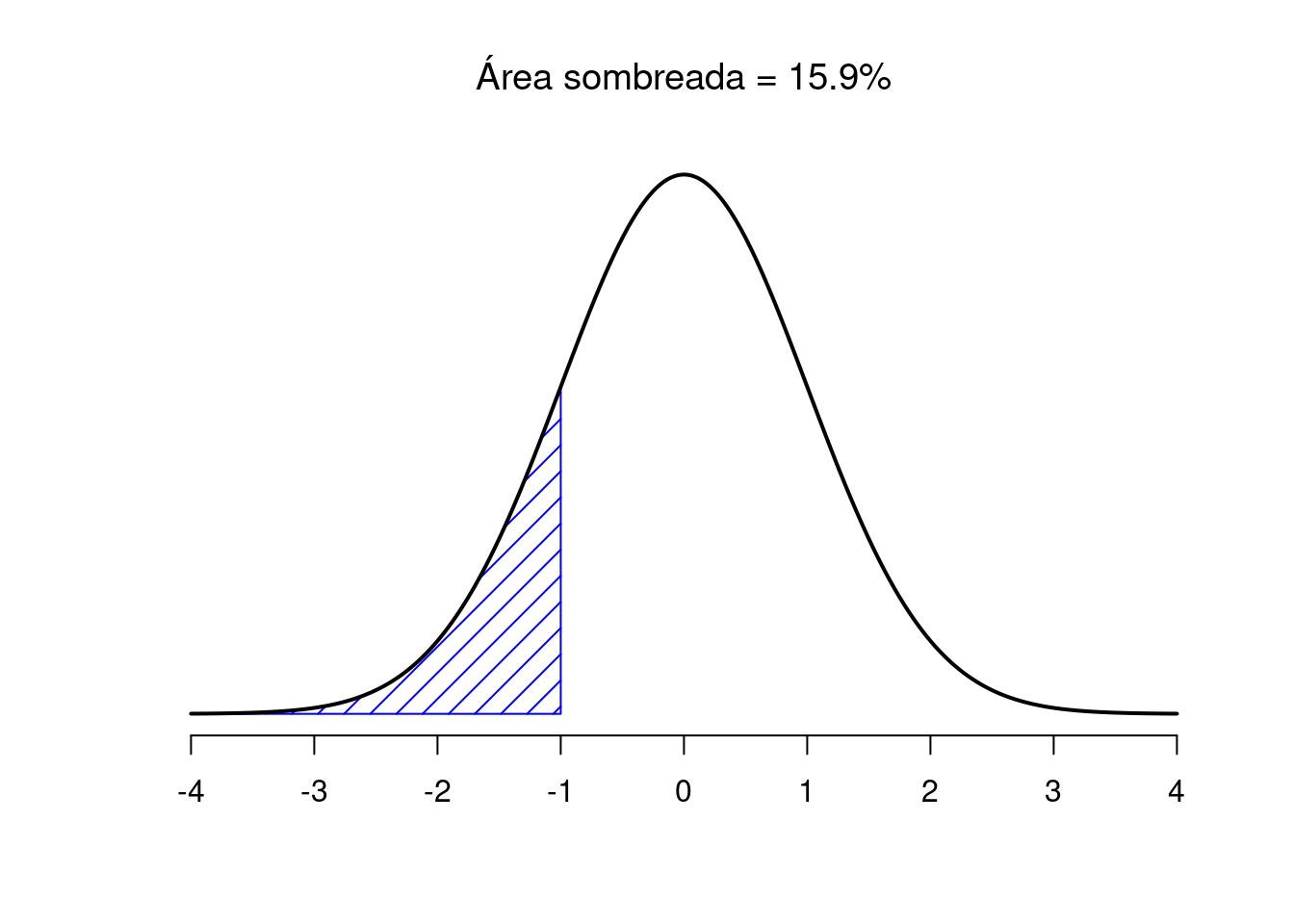
Figura 3.11: Dos ejemplos más de la “idea del área bajo la curva”. Hay un 15.9% de probabilidad de que una observación esté una desviación estándar por debajo de la media o menor.
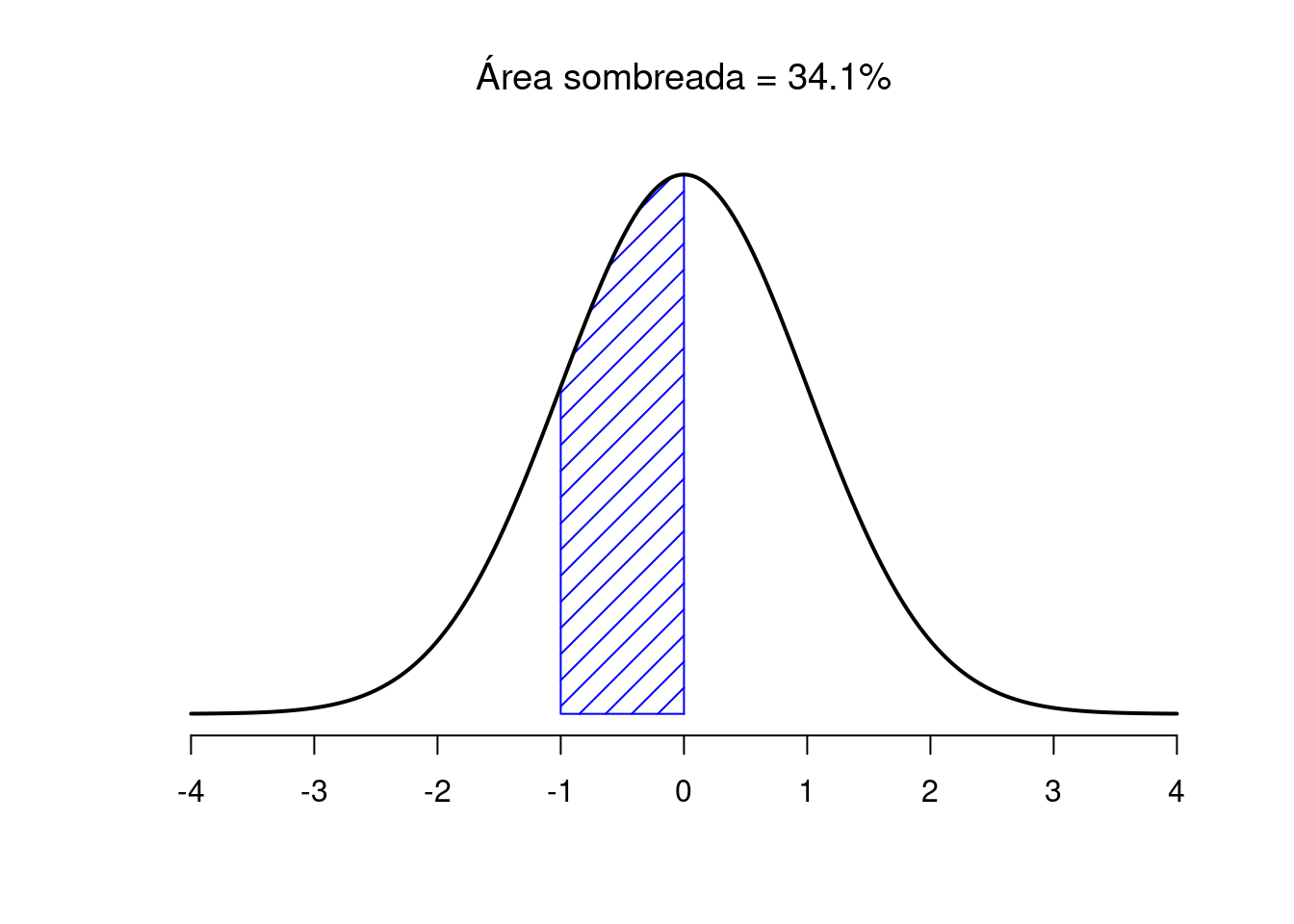
Figura 3.12: Existe una probabilidad del 34,1% de que la observación sea mayor que una desviación estándar por debajo de la media pero aún por debajo de la media. Si suma estos dos números, se obtiene \(15.9 + 34.1 = 50\). Para datos distribuidos normalmente, existe un 50% de probabilidad de que una observación caiga por debajo de la media. Y, por supuesto, eso también implica que hay un 50% de probabilidad de que esté por encima de la media.
3.4 Introduccion a los test de hipótesis
Primero cabe preguntarse por qué intentaríamos hacer inferencias sobre un parámetro de una población basadonos en una muestra, en lugar de simplemente recopilar datos para toda la población, calcular estadísticas que nos interesan y tomar decisiones basadas en eso. La principal razón por la que utilizamos una muestra en lugar de toda la población es porque recopilar datos sobre toda la población es más compicado o en ocasiones impracticable por varios motivos (complejidad, coste, limitación de tiempo, entre muchos otros motivos).2
El objetivo general de una prueba de hipótesis es sacar conclusiones para confirmar o refutar una creencia sobre una población basándonos en un grupo más pequeño de observaciones.
Las pruebas de hipótesis tienen muchas aplicaciones prácticas. Aquí ponemos algunos ejemplos:
- Una media: supongamos que a un político le gustaría le gustaría probar si el salario medio de los trabajadores españoles es diferente de 1200 euros.
- Dos medias:
- Muestras independientes: supongamos que a un profesor le gustaría probar la idoneidad de un nuevo método docente midiendo la nota media para los alumnos de un grupo de control y los del grupo en el que se ha introducido la novedad.
- Muestras pareadas o relacionadas: supongamos que el mismo profesor quisiera probar la idoneidad de este nuevo método de enseñanza pero lo hiciera midiendo los conocimientos de los alumnos antes y después de la explicación.
- Una proporción: supongamos que a un analísta político quisiera comprobar si la proporción de ciudadanos que van a votar por un candidato específico es inferior al 25%.
- Dos proporciones: supongamos que a un geógrafo le gustaría probar si la proporción de visitantes a una playa es diferente entre jóvenes y personas mayores.
- Una variación: supongamos que un ingeniero quisiera probar si una batería tiene una variabilidad en el timpo de carga menor que la indicada en la descripción técnica.
- Dos variaciones: supongamos que, en una fábrica, dos líneas de producción funcionan independientemente una de la otra. El gerente querría probar si los costes del mantenimiento semanal de estas dos cadenas de producción tienen la misma variación.
Por supuesto, hay muchísimas más aplicaciones potenciales y muchas preguntas de investigación pueden responderse gracias a una prueba de hipótesis.
Por lo general, las pruebas de hipótesis se utilizan para responder preguntas de investigación en análisis confirmatorios. Los análisis confirmatorios se refieren a análisis estadísticos donde las hipótesis — deducidas de la teoría — se definen de antemano (preferiblemente antes de la recopilación de datos). En este enfoque, la investigadora tiene una idea específica sobre las variables en consideración y está tratando de ver si su idea, especificada como hipótesis, está respaldada por datos.
Podemos utilizar al menos tres métodos diferentes para realizar una prueba de hipótesis comparando:
- la estadística de prueba con el valor crítico.
- el p-valor con el nivel de significancia \(\alpha\).
- el parámetro objetivo con el intervalo de confianza.
Estos enfoques puede diferir en algunos aspectos pero tienen muchos puntos en común. El uso de uno u otro método es a menudo una cuestión de elección personal o de contexto.
Para los tres métodos, explicaré los pasos necesarios para realizar una prueba de hipótesis desde un punto de vista general y los ilustraré con la siguiente situación:.3
Supongamos que un político quisiera comprobar si el salario medio de los trabajadores españoles es diferente de 1.200 euros.
En la mayoría de las pruebas de hipótesis, la prueba que vamos a utilizar como ejemplo a continuación requiere algunas condiciones. En esta sección asumimos que se cumplen todos los supuestos pero más adelante hablaremos de esto.
3.4.1 Comparando la estadística de prueba con el valor crítico.
Este metodo consiste en reproducir los siguientes 4 pasos:
- Establecer la hipótesis nula y alternativa
- Calcular la estadística de prueba
- Encontrar el valor crítico
- Concluir e interpretar los resultados
3.4.1.1 Estableciendo la hipótesis nula y alternativa
Una prueba de hipótesis primero requiere una suposición sobre un fenómeno o hipótesis, que se deriva de la teoría y la pregunta de investigación.
Dado que una prueba de hipótesis se utiliza para confirmar o refutar una creencia previa, necesitamos formular nuestra creencia de modo que haya una hipótesis nula y una alternativa. Esas hipótesis deben ser mútuamente excluyentes, lo que significa que no pueden ser verdaderas al mismo tiempo. En el contexto, las hipótesis nula y alternativa son así:
- Hipótesis nula \(H_0:\mu=1200\)
- Hipótesis alternativa \(H_1:\mu\ne 1200\)
Al plantear la hipótesis nula y alternativa, tenga en cuenta los siguientes tres puntos:
- Siempre estamos interesados en la población y no en la muestra. Esta es la razón por la que \(H_0\) y \(H_1\) siempre se escribirán en términos de población y no en términos de muestra (en este caso, \(\mu\) y no \(\overline{x}\)).
- La suposición que nos gustaría probar es a menudo la hipótesis alternativa. Si quisieramos probar si el salario medio de los trabajadores españoles es inferior a 1200 euros, habríamos establecido que \(H_0:\mu = 1200\) (o equivalentemente, \(H_0:\mu\ge 1200\)) y \(H_1:\mu<1200\). No hay que confundir la hipótesis nula con la alternativa, o las conclusiones serán diametralmente opuestas.
- La hipótesis nula es a menudo el status quo. Por ejemplo, suponiendo que un empresario quiere probar si el nuevo logo de su marca es mejor valorado que el logo anterior. El status quo es que los dos logos sean igualmente valorados. Suponiendo que un valor mayor es mejor, entonces se escribirá \(H_0:\mu_{nuevo}=\mu_{viejo}\) (o equivalentemente, \(H_0:\mu_{nuevo} - \mu_{viejo} = 0\)) y \(H_1:\mu_{nuevo}>\mu_{viejo}\) (o equivalentemente, \(H_0:\mu_{nuevo} - \mu_{viejo}> 0\)). Por el contrario, si cuanto más bajo mejor, habríamos escrito \(H_0: \mu_{nuevo} = \mu_{viejo}\) (o equivalentemente, \(H_0: \mu_{nuevo} - \mu_{viejo} = 0\)) y \(H_1:\mu_{nuevo} <\mu_{viejo}\) (o equivalentemente, \(H_0: \mu_{nuevo} - \mu_{viejo}<0\)).
3.4.1.2 Calcular la estadística de prueba
La estadística de prueba (o t-stat) es una métrica que indica qué tan extremas son las observaciones en comparación con la hipótesis nula. Cuanto mayor sea el t-stat (en valor absoluto), más extremas serán las observaciones.
Hay varias fórmulas para calcular el t-stat, con una fórmula para cada tipo de prueba de hipótesis: una o dos medias, una o dos proporciones, una o dos varianzas. Esto significa que hay una fórmula para calcular el t-stat para una prueba de hipótesis en una media, otra fórmula para una prueba en dos medias, otra para una prueba en una proporción, etc.4 La única dificultad en este segundo paso es elegir la fórmula adecuada. Tan pronto como se sepa qué fórmula utilizar según el tipo de prueba, simplemente debe aplicársele a los datos. Afortunadamente, las fórmulas para las pruebas de hipótesis en una y dos medias, y una y dos proporciones siguen la misma estructura.
Calcular la estadística de prueba para estas pruebas es similar a escalar una variable aleatoria (un proceso también conocido como “estandarización” o “normalización”) que consiste en restar la media de esa variable aleatoria y dividir el resultado por la desviación estándar:
\[Z = \frac{X - \mu}{\sigma}\] Para estas 4 pruebas de hipótesis (una/dos medias y una/dos proporciones), calcular el estadístico de prueba es como escalar el estimador (calculado a partir de la muestra) correspondiente al parámetro de interés (en la población). Así que básicamente restamos el parámetro objetivo del estimador puntual y luego dividimos el resultado por el error estándar (que es equivalente a la desviación estándar, pero para un estimador).
Si esto no está claro, así es como se calcula la estadística de prueba (\(t_{obs}\)) en nuestro ejemplo (asumiendo que se desconoce la varianza de la población):
\[t_{obs} = \frac{\overline{x} - \mu}{\frac{s}{\sqrt{n}}}\]
dónde:
- \(\overline{x}\) es la media de la muestra (es decir, el estimador)
- \(\mu\) es la media bajo la hipótesis nula (es decir, el parámetro objetivo)
- \(s\) es la desviación estándar de la muestra
- \(n\) es el tamaño de la muestra
- (\(\frac{s}{\sqrt{n}}\) es el error estándar)
Suponiendo que en nuestro caso tenemos una media muestral de 1150 euros (\(\overline{x} = 1150\)), una desviación estándar muestral de 200 euros (\(s=200\)) y un tamaño de muestra de 30 trabajadores (\(n=30\)) y, teniendo en cuenta que la media poblacional (la media bajo la hipótesis nula) es 1200 euros (\(\mu=1200\)), el t-stat quedaría así:
\[t_{obs} = \frac{\overline{x} - \mu}{\frac{s}{\sqrt{n}}} = \frac{1150 - 1200}{\frac{200}{\sqrt{30}}} = -1.369306\]
Aunque las fórmulas son diferentes según el parámetro que esté probando, el valor encontrado para la estadística de prueba nos da una indicación de cuán extremas son nuestras observaciones.
Recordemos este valor de -1.369306 porque se volverá a utilizar al final de este test para compararlo con el valor crítico.
3.4.1.3 Encontrando el valor crítico
Aunque el t-stat nos da una indicación como de extremas son nuestras observaciones, necesitamos comparar este valor con un umbral o valor crítico, que viene dado por una distribución de probabilidad.
De la misma manera que la fórmula para calcular el t-stat es diferente para cada parámetro de interés, la distribución de probabilidad subyacente en la que se basa el valor crítico también es diferente para cada parámetro objetivo. Esto significa que, además de elegir la fórmula apropiada para calcular el t-stat, también necesitamos seleccionar la distribución de probabilidad apropiada dependiendo del parámetro que estemos probando.
Afortunadamente, solo hay 4 distribuciones de probabilidad diferentes para las pruebas de hipótesis cubiertas aquí (recordemos que son una/dos medias, una/dos proporciones y una/dos varianzas):
- Distribución normal estándar:
- prueba en una y dos medias con varianzas de población conocidas.
- prueba en dos muestras donde se conoce la varianza de la diferencia entre las 2 muestras \(\sigma^2_D\)
- prueba en una y dos proporciones (dado que se cumplen algunos supuestos).
- Distribución de Student:
- prueba en una y dos medias con *varianza(s) de población desconocida(s).
- prueba en dos muestras donde la varianza de la diferencia entre las 2 muestras \(\sigma^2_D\) es desconocida.
- Distribución Chi-cuadrado:
- prueba en una varianza.
- Distribution de fisher:
- prueba en dos varianzas.
Cada distribución de probabilidad tiene sus propios parámetros, definiendo su forma y/o ubicación. Los parámetros de una distribución de probabilidad pueden verse como si fuesen marcadores de ADN; lo que significa que la distribución está completamente definida por su(s) parámetro(s).
Volviendo a nuestra investigación, la distribución de probabilidad subyacente de una prueba en una media es la distribución Normal estándar o de Student, dependiendo de si la varianza de la población (no la varianza de la muestra) es conocida o no:
- Si se conoce la varianza de la población \(\rightarrow\), se usa la distribución Normal estándar
- Si la varianza de la población es desconocida \(\rightarrow\), se utiliza la distribución de Student
Si no se proporciona explícitamente la varianza de la población, se puede suponer que es desconocida, ya que no se puede calcular basándonos en una muestra. Si pudiera calcularlo, eso significaría que tiene acceso a toda la población y, en este caso, no tiene sentido realizar una prueba de hipótesis (simplemente podría usar algunas estadísticas descriptivas para confirmar o refutar su creencia dicha hipótesis. En nuestro ejemplo, no se especifica la varianza de la población, por lo que se supone que es desconocida. Por lo tanto, usaremos la distribución de Student.
La distribución Student tiene un parámetro que la define: el número de grados de libertad. El número de grados de libertad depende del tipo de prueba de hipótesis. Por ejemplo, el número de grados de libertad para una prueba en una media es igual al número de observaciones menos uno (\(n-1\)). Sin ir demasiado lejos en los detalles, el \(- 1\) proviene del hecho de que hay una cantidad que se estima (es decir, la media). Siendo el tamaño de la muestra igual a 30 en nuestro ejemplo, los grados de libertad son iguales a \(n -1 = 30-1=29\).
Por último, para encontrar el valor crítico también es necesario conocer el nivel de significancia \(\alpha\), que es la probabilidad de rechazar erróneamente la hipótesis nula aunque en realidad sea verdadera. En este sentido, es un error de tipo I (en contraposición al error de tipo II) que aceptamos para poder sacar conclusiones sobre una población a partir de un subconjunto de ella.
En muchas aplicaciones el nivel de significancia se suele establecer en el 5%. En cambio, en algunos campos (como la medicina o la ingeniería, entre otros), el nivel de significancia también se establece a veces en el 1% para disminuir la tasa de error. Es mejor especificar el nivel de significancia antes de realizar una prueba de hipótesis para evitar la tentación de establecer el nivel de significancia de acuerdo con los resultados (la tentación es aún mayor cuando los resultados están al borde de ser significativos). En nuestro caso, tomamos \(\alpha = 5\% = 0.05\).
Además, queremos probar si el salario medio de los trabajadores españoles es diferente de 1200 euros. Si quisiéramos probar que el salario medio fuera inferior a 1200 euros (\(H_1: \mu <1200\)) o superior a 1200 (\(H_1: \mu>1200\)), habríamos realizado una prueba unilateral. Asegúrese de realizar la prueba correcta (bilateral o unilateral) porque tiene un impacto en cómo encontrar el valor crítico.
Ahora que conocemos la distribución apropiada (distribución de Student), su parámetro (grados de libertad (gl) = 29), el nivel de significancia (\(\alpha\) = 0.05) y la dirección (bilateral), tenemos todo lo que necesitamos para calcular el valor crítico. Podríamos localizar este valor en la tabla estadística correspondiente o directamente lo podríamos calcular con R.
Al observar la fila df = 29 y la columna \(t_.025\) en la tabla de distribución de Student, encontramos un valor crítico de:
\[t_{n-1;\alpha/2} = t_{29; 0.025} = 2.04523\]
Tomamos \(t_{\alpha/2} = t_.025\) y no \(t_\alpha = t_.05\) ya que el nivel de significancia es 0.05 y estamos haciendo una prueba bilateral (de dos lados; \(H_1:\mu\ne 1200\)), por lo que la tasa de error de 0.05 debe dividirse en 2 para encontrar el valor crítico a la derecha de la distribución. Dado que la distribución de Student es simétrica, el valor crítico a la izquierda de la distribución es simplemente: -2.04523.
Visualmente, la tasa de error de 0.05 se divide en dos partes:
- 0,025 a la izquierda de -2,04523 y
- 0,025 a la derecha de 2,04523
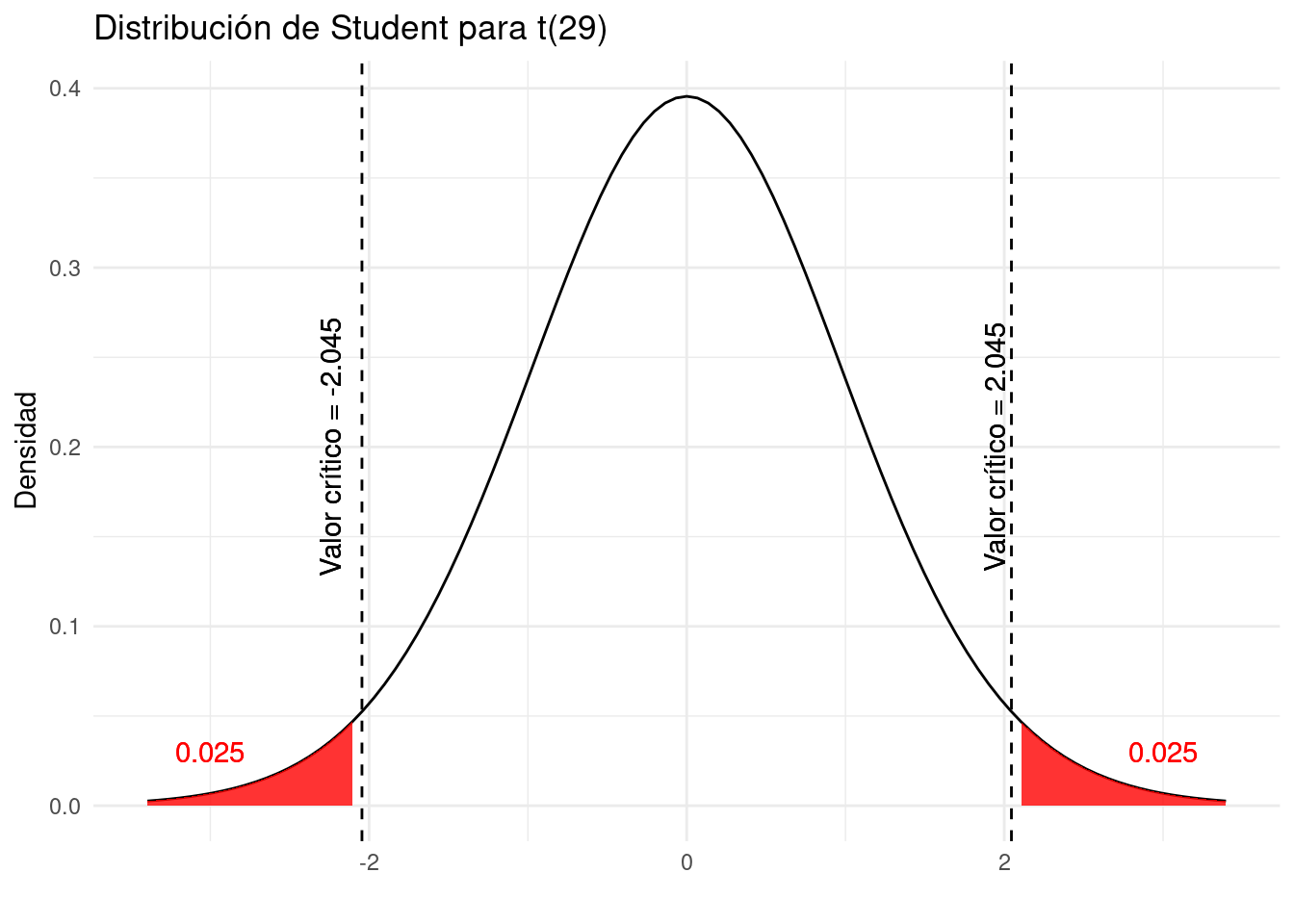
Al igual que en el apartado anterior, cabe recordar estos valores críticos de -2,045 y 2,045 el último paso.
Las áreas sombreadas en rojo en el gráfico anterior también se conocen como regiones de rechazo.
Estos valores críticos también se pueden encontrar en R, gracias a la función qt ():
## [1] -2.04523## [1] 2.04523Como se ha visto en el tema sobre distribuciones de probabilidad, la función qt () se usa para la distribución de Student (q significa cuantil yt para Student). Cabe recordar que hay otras funciones que acompañan a las diferentes distribuciones:
qnorm ()para la distribución Normalqchisq ()para la distribución Chi-cuadradoqf ()para la distribución de Fisher
3.4.1.4 Conclusión e interpretación de los resultados
Las únicas dos posibilidades al concluir una prueba de hipótesis son:
- Rechazo de la hipótesis nula, o
- No rechazo de la hipótesis nula
En nuestro ejemplo sobre los salarios de los españoles, recordamos que hemos determinado que el:
- el
t-states -1.369306, y - los valores críticos son -2.04523 y 2.04523
Recordemos que:
- el t-stat da una indicación de cuán extrema es nuestra muestra en comparación con la hipótesis nula
- los valores críticos son el umbral a partir del cual el t-stat se considera demasiado extremo
Para comparar el t-stat con los valores críticos de manera gráfica:
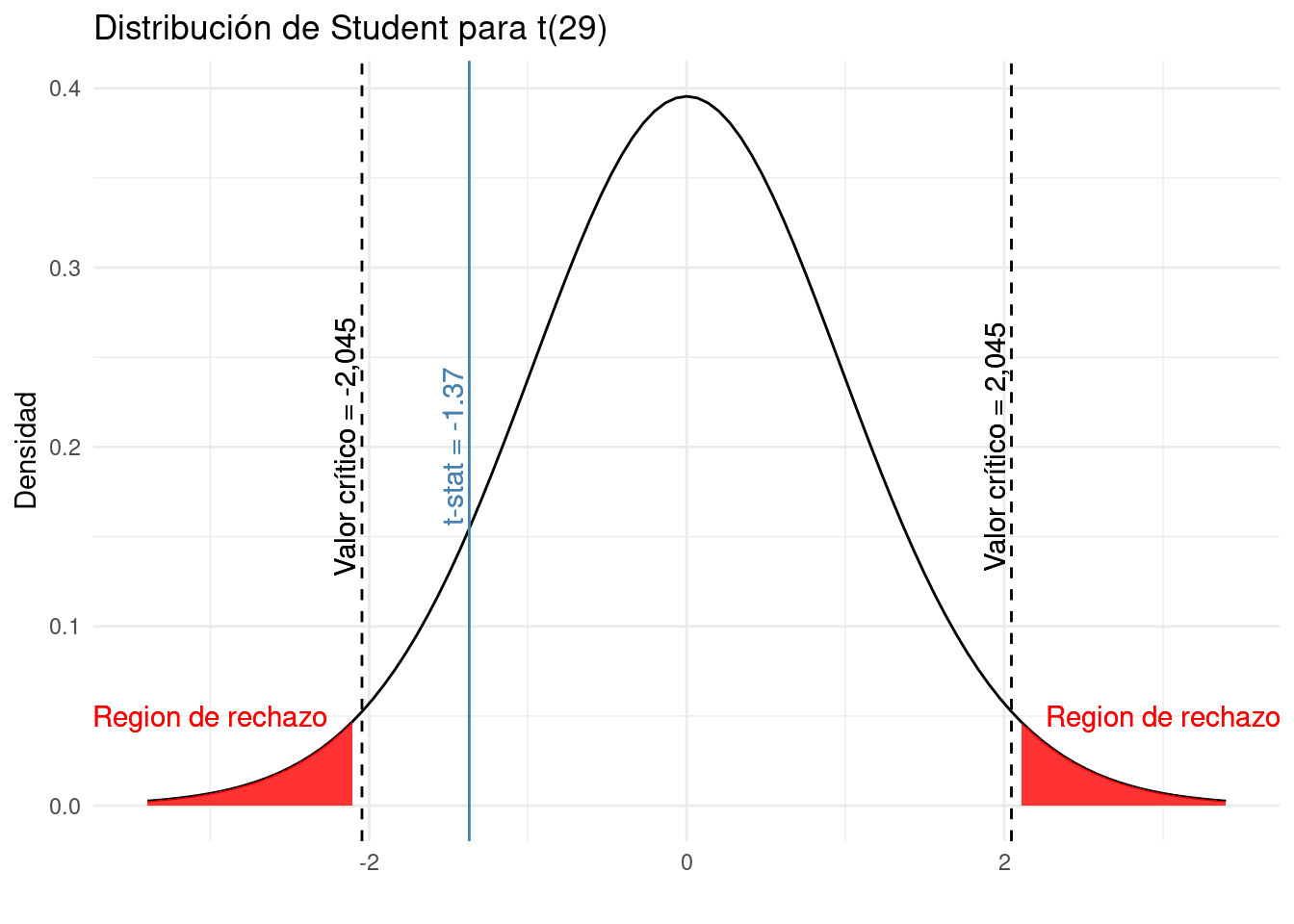
Los dos valores críticos forman las regiones de rechazo (las áreas sombreadas en rojo):
- de \(-\infty\) a -2.045, y
- de 2.045 a \(\infty\)
Si el t-stat se encuentra dentro de una de estas regiones, rechazamos la hipótesis nula. Por el contrario, si t-stat no se encuentra dentro de ninguna de las regiones, no rechazamos la hipótesis nula.
Como podemos ver en el gráfico anterior, el t-stat es menos extremo que el valor crítico. En conclusión, no rechazamos la hipótesis nula de que \(\mu = 1200\).
Esta es la conclusión en términos estadísticos, pero no tienen sentido sin una interpretación adecuada. Por tanto, es una buena práctica interpretar también el resultado en el contexto del problema:
Con un nivel de significancia del 5%, no rechazamos la hipótesis de que el salario medio de los trabajadores españoles es de 1200 euros.
¿Qué significa esto realmente? Dicho de otro modo:
“nosotros no rechazamos la hipótesis nula” y “nosotros no rechazamos la hipótesis de que el salario medio de los trabajadores españoles es igual a 1200 euros”. No escribimos “aceptamos o estamos de acuerdo con la hipótesis nula” ni “el salario medio de los trabajadores españoles es de 1200 euros”.
En los test de hipótesis, llegamos a una conclusión sobre la población a partir de una muestra. Por tanto, siempre existe cierta incertidumbre y no podemos decir que estemos seguros al 100% de que nuestra conclusión sea correcta.
Quizás sea el caso de que el salario medio de los trabajadores españoles sea en realidad diferente a 1200 euros, pero no lo pudimos demostrar con los datos disponibles. Si tuviéramos más observaciones hubiéramos rechazado la hipótesis nula (dado que todo lo demás es igual, un tamaño de muestra más grande implica un t-stat más extremo). O puede darse el caso de que, incluso con más observaciones, no hubiéramos rechazado la hipótesis nula porque el salario de los trabajadores españoles en realidad se acerca a los 1200 euros. Con los datos disponibles no podemos distinguir entre estas dos posibilidades. Simplemente debemos admitir que no encontramos suficiente evidencia en contra de la hipótesis de partida, pero tampoco concluimos que la media sea igual a 1200 euros.
3.4.2 Comparando el p-valor con el nivel de significancia \(\alpha\)
Este método consiste en los siguientes pasos:
- Enunciar las hipótesis nula y alternativa
- Calcular la estadística de prueba (
t-stat). - Calcular el p-valor
- Concluir e interpretar los resultados
En este segundo método que utiliza el valor p, los dos primeros pasos son similares a los del primer método, mientras que la interpretación de los resultados tiene algunos puntos en común.
3.4.2.1 Establecer las hipótesis
Las hipótesis de investigación (nula y alternativa) siguen siendo las mismas:
- \(H_0:\mu= 1200\)
- \(H_1:\mu\ne 1200\)
3.4.2.2 Calcular la estadística de prueba
Cabe recordar que la fórmula del estadístico t es diferente según el tipo de prueba de hipótesis (una o dos medias, una o dos proporciones, una o dos varianzas). En nuestro caso de una sola media con varianza desconocida, tenemos que:
\[t_{obs} = \frac{\overline{x} - \mu}{\frac{s}{\sqrt{n}}} = \frac{1150 - 1200}{\frac{200}{\sqrt{30}}} = -1.369306\]
3.4.2.3 Calculo del valor p
El p-valor es la probabilidad (de 0 a 1) de observar una muestra al menos tan extrema como la que observamos si la hipótesis nula fuera cierta. Dicho de otro modo: ¿cómo de probable es la hipótesis nula?. También se define como el nivel de significancia más pequeño para el cual los datos indican el rechazo de la hipótesis nula.
Formalmente, el valor p es el área más allá del estadístico de prueba. Como estamos haciendo una prueba bidireccional, el valor p es, por lo tanto, la suma del área por encima de 1,369306 y por debajo de -1,369306.
Visualmente, el valor p es la suma de las dos áreas sombreadas en azul en la siguiente gráfica:
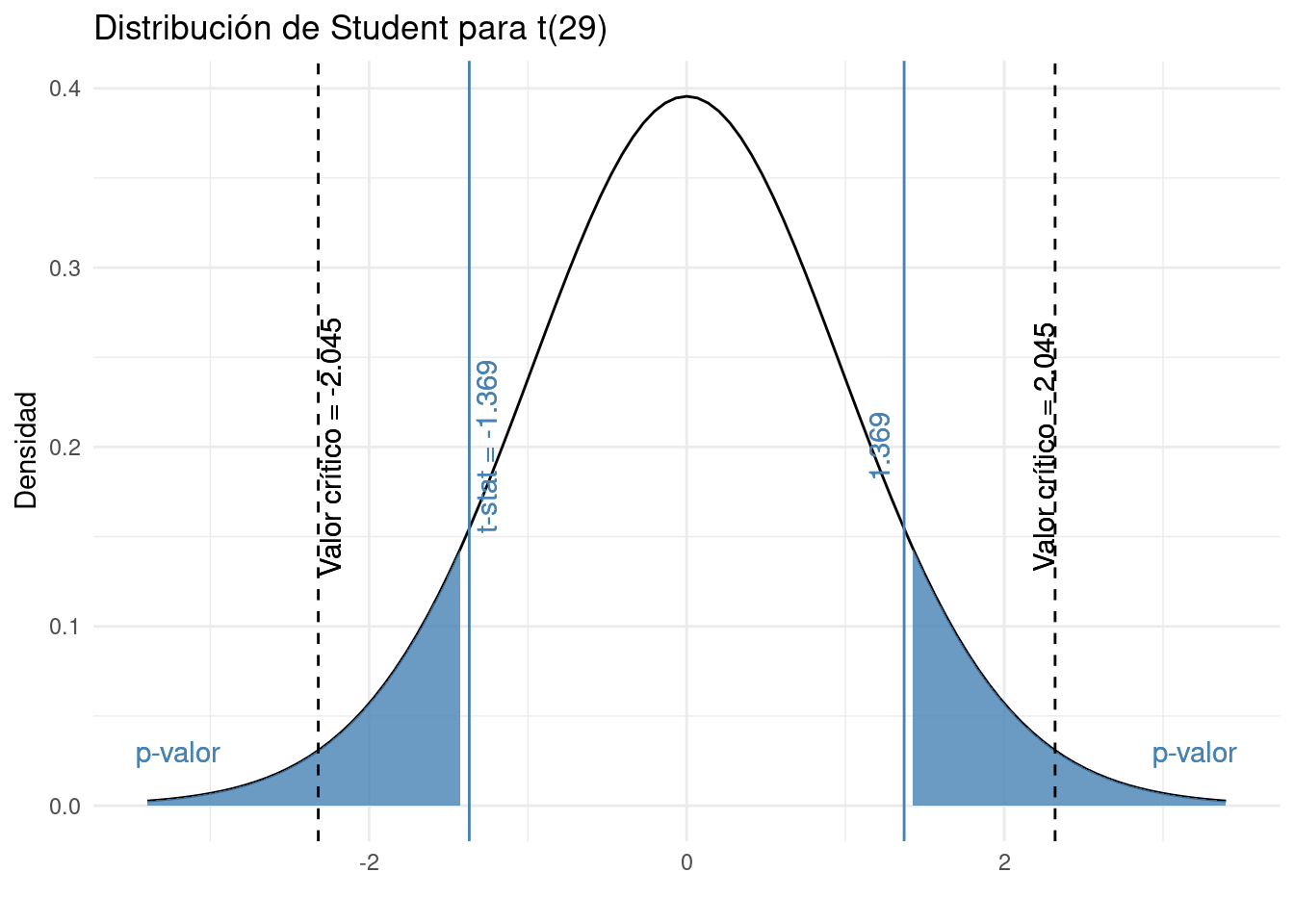
El valor p se puede obtener también con tablas estadísticas o es posible calcularlo con precisión en R con la función pt():
p_val <- pt(-1.369306, df = 29, lower.tail = TRUE) + pt(1.369306, df = 29, lower.tail = FALSE)
p_val## [1] 0.1814156## [1] 0.1814156El valor p es 0.1814, que indica que hay un 18.14% de probabilidad de observar una muestra al menos tan extrema como la observada si el hipótesis nula eran verdaderas. Esto ya nos da una pista sobre si nuestro t-stat es demasiado extremo o no (y, por lo tanto, si nuestra hipótesis nula es probable o no).
Como la función qt() para encontrar el valor crítico, usamos pt() para encontrar el valor p porque la distribución subyacente es la distribución de Student. En otros casos se utilizarían las funciones pnorm (), pchisq () y pf () para las otras distribuciones mencionadas anteriormente (Normal, Chi-cuadrado y Fisher).
3.4.2.4 Concluir e interpretar los resultados
Finalmente, hay que comparar el valor p que acabamos de calcular con el nivel de significancia \(\alpha\). Como para todas las pruebas estadísticas:
- Si el p-valor es menor que \(\alpha\) (p-valor\(<0.05\)), entonces \(H_0\) es poco probable \(\rightarrow\) rechazamos la hipótesis nula.
- Si el p-valor es mayor que o igual a \(\alpha\) (p-valor \(\ge 0.05\)), entonces \(H_0\) es probable \(\rightarrow\) no podemos rechazar la hipótesis nula.
No importa si tomamos en consideración el p-valor exacto (es decir, 0.1814) o el acotado (0.05 <p-valor <0.10), es mayor que 0.05, entonces no rechazamos la hipótesis nula. En el contexto del problema, no rechazamos la hipótesis nula de que el salario medio de los trabajadores españoles es igual a 1200 euros.
El resultado obtenido ha sido el mismo que en el primer método. Evidentemente, debería dar lo mismo si se usan los mismos datos y con el mismo nivel de significancia.
3.4.3 Comparación del parámetro objetivo con el intervalo de confianza
Este método consiste en calcular primero el intervalo de confianza y comparar sobre éste el parámetro objetivo (el parámetro bajo la hipótesis nula). Podemos distinguir tres pasos:
- Enunciar las hipótesis nula y alternativa
- Calcular el intervalo de confianza
- Concluir e interpretar los resultados
También se pueden apreciar varias similitudes con los métodos anteriores.
3.4.3.1 Enunciar las hipótesis
Nuevamente, las hipótesis nula y alternativa siguen siendo las mismas:
- \(H_0:\mu = 1200\)
- \(H_1:\mu\ne 1200\)
3.4.3.2 Calcular el intervalo de confianza
Al igual que los test de hipótesis, los intervalos de confianza son una herramienta bien conocida en la estadística inferencial. El intervalo de confianza es un procedimiento de estimación que produce un intervalo que contiene el parámetro verdadero con una cierta probabilidad.
De la misma manera que existe una fórmula para cada tipo de prueba de hipótesis al calcular las estadísticas de la prueba, existe una fórmula para cada tipo de intervalo de confianza. La fórmula para calcular un intervalo de confianza en una media \(\mu\) (con varianza poblacional desconocida): \[ (1-\alpha)\% \text{ IC para } \mu=\overline{x}\pm t_{\alpha/2, n - 1}\frac{s}{\sqrt{n}} \] donde \(t_{\alpha/2, n-1}\) se encuentra en la tabla de distribución de Student o se puede calcular con R (y es similar al valor crítico encontrado en el primer método).
Dados nuestros datos y con \(\alpha= 0.05\), tenemos que: \[ \begin{aligned} 95\%\text{ IC para } \mu &= \overline{x} \pm t_{\alpha/2, n - 1} \frac{s}{\sqrt{n}} \\ &= 1150 \pm 2.045 \frac{200}{\sqrt{30}} \\ &= [1075,33; 1224,67] \end{aligned} \]
El intervalo de confianza del 95% para \(\mu\) es [1075,33; 1224,67] euros. ¿Qué significa este intervalo de confianza del 95%?
Sabemos que este procedimiento de estimación tiene una probabilidad del 95% de producir un intervalo que contenga la media verdadera \(\mu\). En otras palabras, si construimos muchos intervalos de confianza (con diferentes muestras del mismo tamaño), el 95% de ellos incluirá la media de la población (el verdadero parámetro). Del mismo modo el 5% de estos intervalos de confianza no cubrirán la media real.
Si desea disminuir este último porcentaje, puede disminuir el nivel de significancia (por ejemplo \(\alpha= 0.01\)). En igualdad de condiciones, esto disminuirá el rango del intervalo de confianza y, por lo tanto, aumentará la probabilidad de que incluya el parámetro verdadero.
3.4.3.3 Conclusión e interpretación de los resultados
Finalmente, hay comparar el intervalo de confianza con el valor del parámetro objetivo (el valor cuestionado por la hipótesis nula):
- Si el intervalo de confianza no incluye el valor hipotético, \(H_0\) es poco probable \(\rightarrow\) rechazamos la hipótesis nula.
- Si el intervalo de confianza incluye el valor hipotético, \(H_0\) es probable \(\rightarrow\), no rechazamos la hipótesis nula
En nuestro ejemplo:
- el valor hipotético es 1200 (desde \(H_0:\mu= 1200\))
- 1200 se incluye en el intervalo de confianza del 95%, ya que va de 1075,33 a 1224,67 euros
- Entonces no rechazamos la hipótesis nula de que el salario medio de los trabajadores españoles sea de 1200 euros.
Por supuesto, la conclusión es equivalente a la que se había llegado por los otros dos métodos. Esto debe ser así, ya que usamos los mismos datos y el mismo nivel de significancia \(\alpha\) para los tres métodos.
3.4.4 Dos tipos de errores
Antes de entrar en detalles sobre cómo se construye una prueba estadística, es útil comprender la filosofía detrás de ella. Idealmente, nos gustaría construir nuestra prueba de modo que nunca cometamos errores. Desafortunadamente, dado que el mundo es caótico, esto no es posible. A veces simplemente tienes mala suerte: por ejemplo, supongamos que lanzas una moneda 10 veces seguidas y sale cara las 10 veces. Eso se parece una evidencia muy fuerte de que la moneda está trucada, pero, por supuesto, hay una probabilidad de 1 entre 1024 de que esto suceda incluso si la moneda fuera completamente normal. En otras palabras, en la vida real siempre tenemos que aceptar que existe la posibilidad… Como consecuencia, el objetivo detrás de las pruebas de hipótesis estadísticas no es eliminar errores, sino minimizarlos.
Debemos ser un poco más precisos sobre lo que entendemos por “errores”. En primer lugar se da el caso de que la hipótesis nula es verdadera o es falsa; y nuestra prueba rechazará la hipótesis nula o la retendrá. ^[Un comentario aparte con respecto al lenguaje que usa para hablar sobre la prueba de hipótesis. En primer lugar, una cosa que realmente desea evitar es la palabra “probar”: una prueba estadística realmente no prueba que una hipótesis sea verdadera o falsa. La prueba implica certeza pero las estadísticas significan nunca tener que decir que estás seguro. Pueden pasar una de cuatro cosas:
| Mantener \(H_0\) | Mantener \(H_0\) | |
|---|---|---|
| \(H_0\) es verdadero | Decisión correcta | Error (Tipo I) |
| \(H_0\) es falso | Error (tipo II) | Decisión correcta |
Como consecuencia, en realidad hay dos tipos diferentes de error. Si rechazamos una hipótesis nula que sea realmente cierta, entonces hemos cometido un error de tipo I. Por otro lado, si mantenemos la hipótesis nula cuando en realidad es falsa, entonces hemos cometido un error tipo II. En juicio penal donde se busca establecer “más allá de toda duda razonable” que el acusado es culpable. Todas las reglas probatorias están (en teoría, al menos) diseñadas para garantizar que (casi) no haya posibilidad de condenar injustamente a un acusado inocente. El juicio está diseñado para proteger los derechos de un acusado: como dijo el famoso jurista inglés William Blackstone, es “mejor que escapen diez culpables que sufra un inocente”. En otras palabras, un juicio penal no trata los dos tipos de error de la misma manera ~ … castigar al inocente se considera mucho peor que dejar en libertad al culpable. Una prueba estadística es prácticamente lo mismo: el principio de diseño más importante de la prueba es controlar la probabilidad de un error de tipo I, para mantenerla por debajo de una probabilidad fija. Esta probabilidad, que se denota \(\alpha\), se denomina nivel de significancia de la prueba (o, a veces, el tamaño de la prueba). Y lo diré de nuevo, porque es tan fundamental para toda la configuración ~ … se dice que una prueba de hipótesis tiene un nivel de significancia \(\alpha\) si la tasa de error de tipo I no es mayor que \(\alpha\) .
Entonces, ¿qué pasa con la tasa de error de tipo II? Bueno, también nos gustaría mantenerlos bajo control, y denotamos esta probabilidad por \(\beta\). Sin embargo, es mucho más común referirse a la potencia de la prueba, que es la probabilidad con la que rechazamos una hipótesis nula cuando realmente es falsa, que es \(1-\beta\). Para ayudar a mantener esto claro, aquí está la misma tabla nuevamente, pero con los números relevantes agregados:
| no descartar \(H_0\) | descartar \(H_0\) | |
|---|---|---|
| \(H_0\) es verdadera | \(1-\alpha\) (probabilidad de mantener) | \(\alpha\) (tasa de error tipo I) |
| \(H_0\) es falsa | \(\beta\) (tasa de error tipo II) | \(1-\beta\) (potencia del test) |
Una prueba de hipótesis “potente” es aquella que tiene un valor pequeño de \(\beta\), mientras mantiene \(\alpha\) fijo en algún (pequeño) nivel deseado. Por convención, los científicos utilizan tres niveles \(\alpha\) diferentes: \(.05\), \(.01\) y \(.001\). Observad la asimetría aquí ~ … las pruebas están diseñadas para asegurar que el nivel \(\alpha\) se mantenga pequeño, pero no hay garantía correspondiente con respecto a \(\beta\). Ciertamente nos gustaría que la tasa de error de tipo II fuera pequeña, y tratamos de diseñar pruebas que la mantengan pequeña, pero esto es muy secundario a la abrumadora necesidad de controlar la tasa de error de tipo I.
3.5 Test de hipótesis en R: cálculo e informes
3.6 Un ejemplo sobre brecha salarial entre géneros
3.7 ANOVA
3.8 Algunas consideraciones finales
3.8.1 ¿Cuando no se necesita inferencia?
Hemos analizado varios ejemplos sobre cómo realizar inferencias estadísticas: realización de test de hipótesis y construcción de intervalos de confianza. Antes de empezar a realizar un experimento, siempre es necesario realizar un análisis exploratorio de los datos. Este primer vistazo siempre puede ayudar a intuir sobre lo que los métodos estadísticos como los intervalos de confianza y las pruebas de hipótesis pueden decirnos (y lo que no pueden). En los apartados anteriores hemos querido explicar cómo funciona la inferencia pero no nos hemos preguntado si era realmente necesaria.
Consideremos un ejemplo. Supongamos que estamos interesados en la siguiente pregunta: De todos los vuelos que salen de un aeropuerto de la ciudad de Nueva York, ¿los vuelos de Hawaiian Airlines están en el aire por más tiempo que los vuelos de Alaska Airlines? Además, supongamos que los vuelos de 2013 son una muestra representativa de todos esos vuelos. Entonces podemos usar el dataframe flights disponible en el paquete nycflights13 para responder nuestra pregunta. Filtremos este dataframe para incluir solo a Hawaiian y Alaska Airlines usando sus códigos de “operador” “HA” y “AS”:
library(tidyverse)
library(nycflights13)
flights_sample <- flights %>%
filter(carrier %in% c("HA", "AS"))Hay dos posibles métodos de inferencia estadística que podríamos utilizar para responder a estas preguntas. Primero, podríamos construir un intervalo de confianza del 95% para la diferencia en las medias poblacionales \(\mu_{HA}-\mu_{AS}\), donde \(\mu_{HA}\) es el tiempo de vuelo medio de todos los vuelos de Hawaiian Airlines y \(\mu_{AS}\) es el tiempo medio de vuelo de los vuelos de Alaska Airlines. Luego podríamos verificar si la totalidad del intervalo es mayor que 0, sugiriendo que \(\mu_{HA} - \mu_{AS}> 0\), o, en otras palabras, sugiriendo que \(\mu_{HA}> \mu_{AS}\). En segundo lugar, podríamos realizar una prueba de hipótesis de la hipótesis nula \(H_0:\mu_{HA} - \mu_{AS} = 0\) frente a la hipótesis alternativa \(H_A:\mu_{HA}-\mu_{AS}>0\).
Construyamos primero una visualización exploratoria como acabamos de sugerir. Dado que air_time es numérico y carrier es categórico, un diagrama de caja (boxplot) puede mostrar la relación entre estas dos variables (ver la Figura 3.13).
ggplot(data = flights_sample, mapping = aes(x = carrier, y = air_time)) +
geom_boxplot() +
labs(x = "Carrier", y = "Air Time")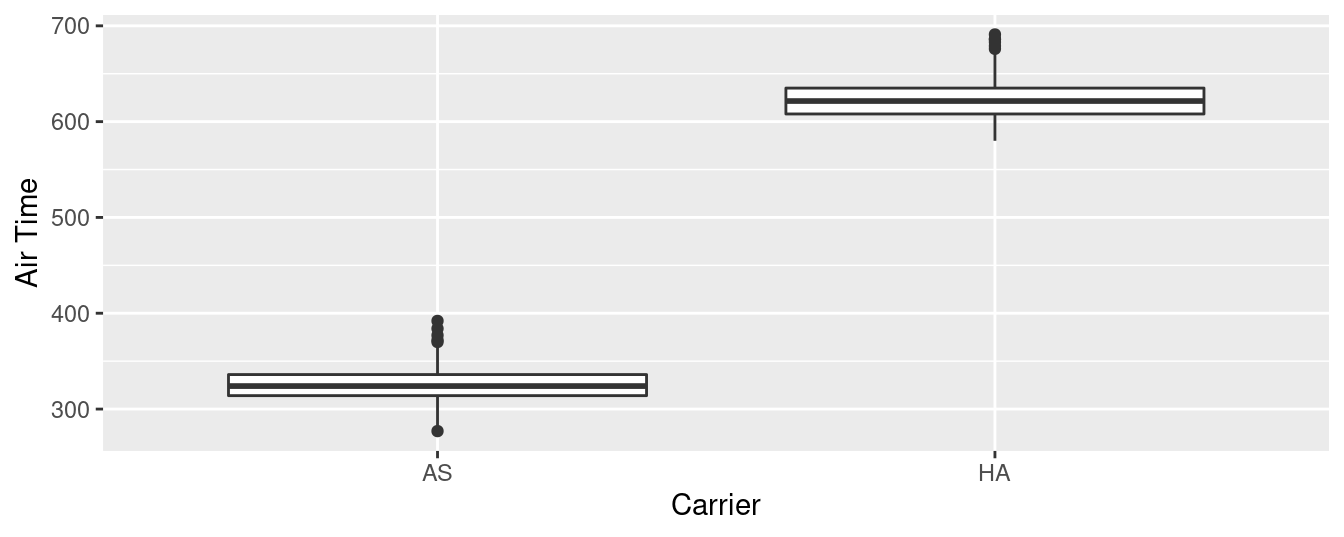
Figura 3.13: Air time for Hawaiian and Alaska Airlines flights departing NYC in 2013.
No es necesario ser un experto en estadísticas para saber que Alaska Airlines y Hawaiian Airlines tienen horarios aéreos significativamente diferentes. ¡Los dos diagramas de caja ni siquiera se superponen! La construcción de un intervalo de confianza o la realización de una prueba de hipótesis, francamente, no proporcionaría mucha más información que la Figura 3.13.
Investiguemos por qué observamos una diferencia tan clara entre estas dos aerolíneas que utilizan la manipulación de datos. Primero agrupemos por las filas de vuelos_muestra no solo portransportista sino también por destino dest. Posteriormente, calcularemos dos estadísticas resumidas: el número de observaciones usando n () y el tiempo medio de transmisión:
flights_sample %>%
group_by(carrier, dest) %>%
summarize(n = n(), mean_time = mean(air_time, na.rm = TRUE))## # A tibble: 2 x 4
## # Groups: carrier [2]
## carrier dest n mean_time
## <chr> <chr> <int> <dbl>
## 1 AS SEA 714 326.
## 2 HA HNL 342 623.Resulta que desde la ciudad de Nueva York en 2013, Alaska solo voló a “SEA” (Seattle) desde la ciudad de Nueva York (NYC) mientras que Hawaiian solo voló a “HNL” (Honolulu) desde Nueva York. Dada la clara diferencia en la distancia entre la ciudad de Nueva York y Seattle y la ciudad de Nueva York a Honolulu, no es sorprendente que observemos tiempos de vuelo tan diferentes (_ estadísticamente significativamente diferentes_, de hecho) en los vuelos.
Este es un claro ejemplo de que no es necesario hacer nada más que un simple análisis exploratorio de datos utilizando visualización de datos y estadísticas descriptivas para llegar a una conclusión adecuada. Por lo tanto, es recomendable empezar siempre por realizar un análisis exploratorio con estadísticas descriptivas antes de aplicar inferencia estadística.
3.8.2 Problemas con los p-valores
Además de los muchos malentendidos comunes sobre las pruebas de hipótesis y los valores de \(p\) que hemos comentado al explicar la interpretación de las pruebas de hipótesis, otra consecuencia desafortunada del uso ampliado de los valores de \(p\) y las pruebas de hipótesis es un fenómeno conocido como “p-hacking”, que es es el acto de “seleccionar” sólo los resultados que son “estadísticamente significativos” y descartar los que no lo son, aunque sea a expensas de las ideas científicas. Hay muchos artículos escritos recientemente sobre malentendidos y problemas con los valores de \(p\). Le recomendamos que consulte algunos de ellos:
- Malentendidos de los valores de \(p\)
- Qué debate más nerd sobre los valores de \(p\) sobre la ciencia y cómo solucionarlo
- Los estadísticos emiten una advertencia sobre el uso indebido de los valores de \(p\)
- No puede confiar en lo que lee sobre nutrición
- Una letanía de problemas con valores p
Tales problemas se estaban volviendo tan recurrentes que la Asociación Estadounidense de Estadística (ASA) emitió una declaración en 2016 titulada, “Declaración de la ASA sobre la importancia estadística y los valores de \(p\)” con seis principios subyacentes al uso e interpretación adecuados de los valores de \(p\). La ASA publicó esta guía sobre los valores de \(p\) para mejorar la conducta y la interpretación de la ciencia cuantitativa y para informar el creciente énfasis en la reproducibilidad de la investigación científica.
Quizás el uso de intervalos de confianza para la inferencia estadística permita evitar ciertos malentendidos. Sin embargo, en muchos campos todavía se usan exclusivamente valores de \(p\) para la inferencia estadística y esta es una razón para incluirlos en este texto.
3.9 Ejercicios
3.9.1 Distribución Binomial
En nuestro municipio hay 500 hombres de la misma edad y con buena salud. Según las estadísticas actuales, la probabilidad de que estas personas vivan 30 años o más es de 2/3. Hay que hallar las probabilidades de que dentro de esos 30 años vivan
- Los 500 hombres.
- Al menos 300 de ellos.
- 200 hombres
3.9.2 Distribución Normal
El ayuntamiento consume una media de 80 \(kWh/hab/a\), con una desviación estándard de 14\(kWh/hab/a\). Hay que calcular:
- La probabilidad de que este año hagan falta entre 75 y 90 (\(p(75 \leqslant x \leqslant 90)\)).
- La probabilidad de que hagan falta 75 o menos (\(p(75 \leqslant x\)).
- Describid en un párrafo alguna variable municipal que se pueda ajustar a una distribución normal y haced la comprobación.
Por ejemplo, una investigación podría consistir en conocer si la población de la provincia de Tarragona está satisfecha con el nuevo plan de movilidad. Si pudiéramos preguntar a toda la población en un período de tiempo razonable, no haríamos ninguna estadística inferencial. No obstante, aún habria que decidir que preguntas se les hace para entender mejor el motivo de su grado de satisfacción, complicando y encareciendo aún más la encuesta.↩︎
Puede ver más o menos pasos en otros artículos o libros de texto, dependiendo de si estos pasos son detallados o concisos. Sin embargo, la prueba de hipótesis debe seguir el mismo proceso independientemente del número de pasos↩︎
Incluso hay diferentes fórmulas dentro de cada tipo de prueba, dependiendo de si se cumplen o no algunos supuestos.↩︎