Capítulo 5 Regresión lineal

El objetivo de este capítulo es presentar la regresión lineal, la herramienta estándar en la que confían los estadísticos al analizar la relación entre los predictores y los resultados. Los modelos de regresión lineal son básicamente una versión un poco más elegante de la correlación de Pearson (Sección @ref (correlation)) aunque, como veremos, los modelos de regresión son herramientas mucho más poderosas.

5.1 ¿Qué es un modelo de regresión lineal?

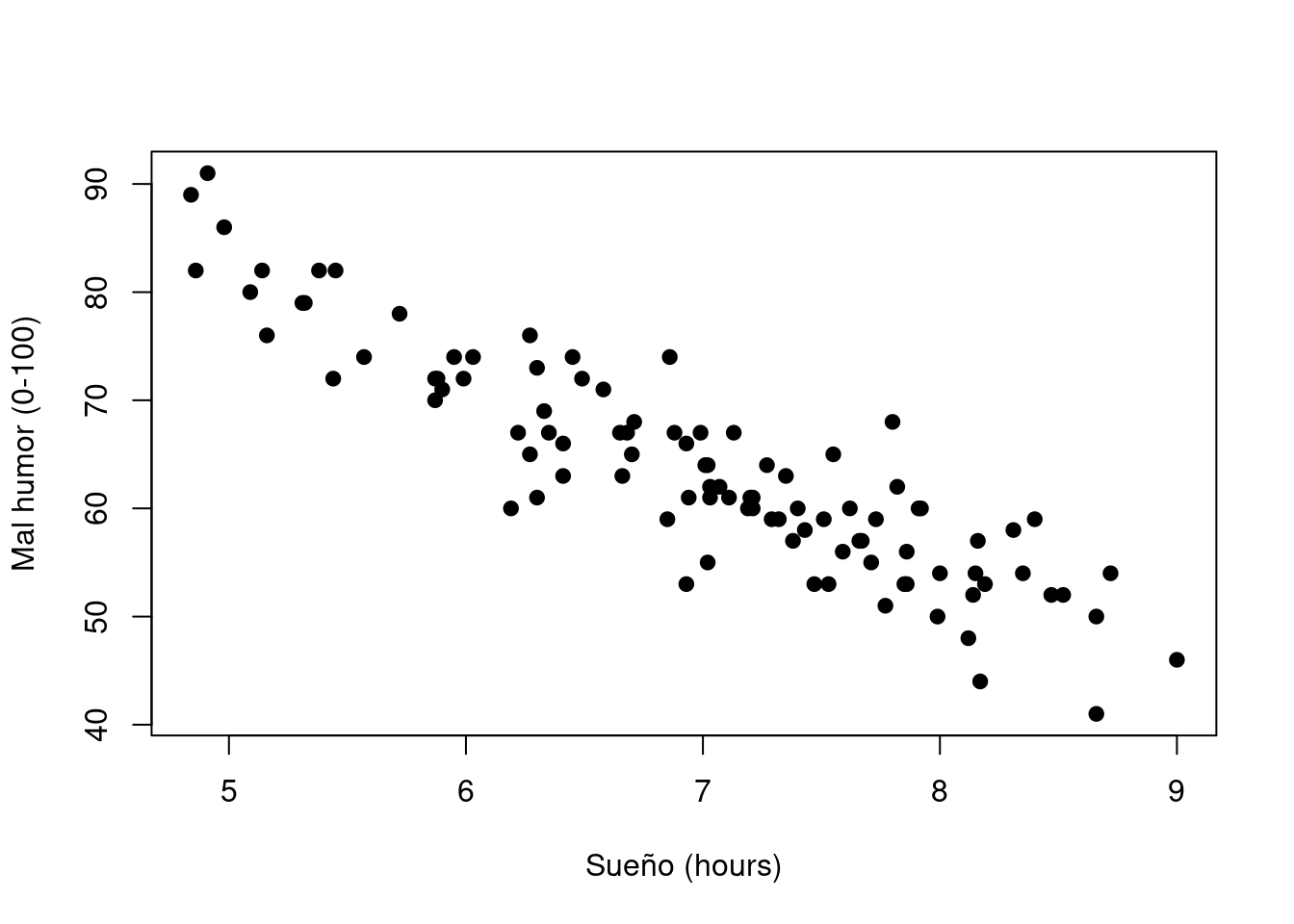
Figura 5.1: Diagrama de dispersión que muestra el mal humor en función de las horas de sueño.

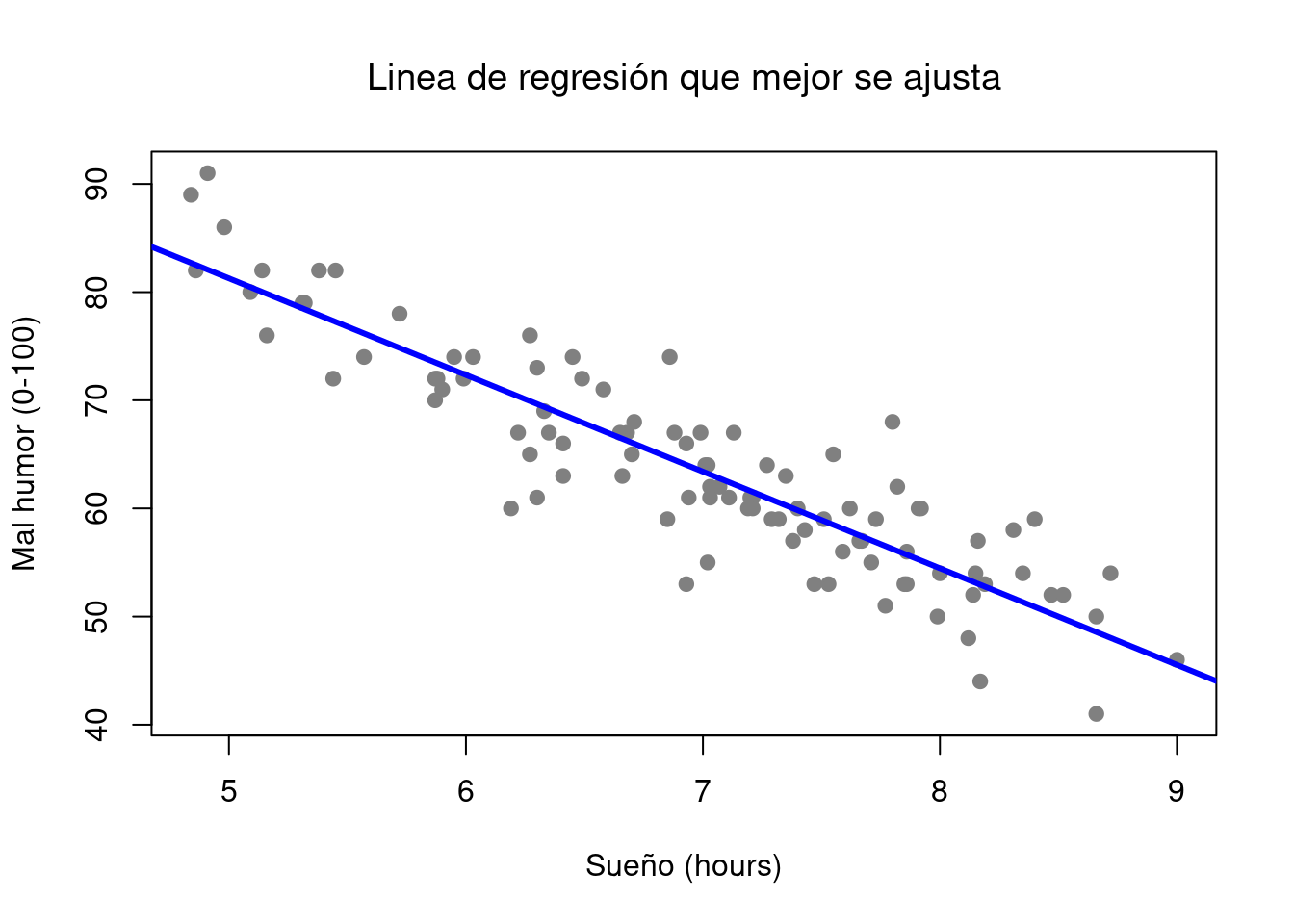
Figura 5.2: El panel a muestra el diagrama de dispersión del mal humor del sueño desde arriba con la línea de regresión que mejor se ajusta dibujada en la parte superior. No es sorprendente que la línea pase por el medio de los datos.

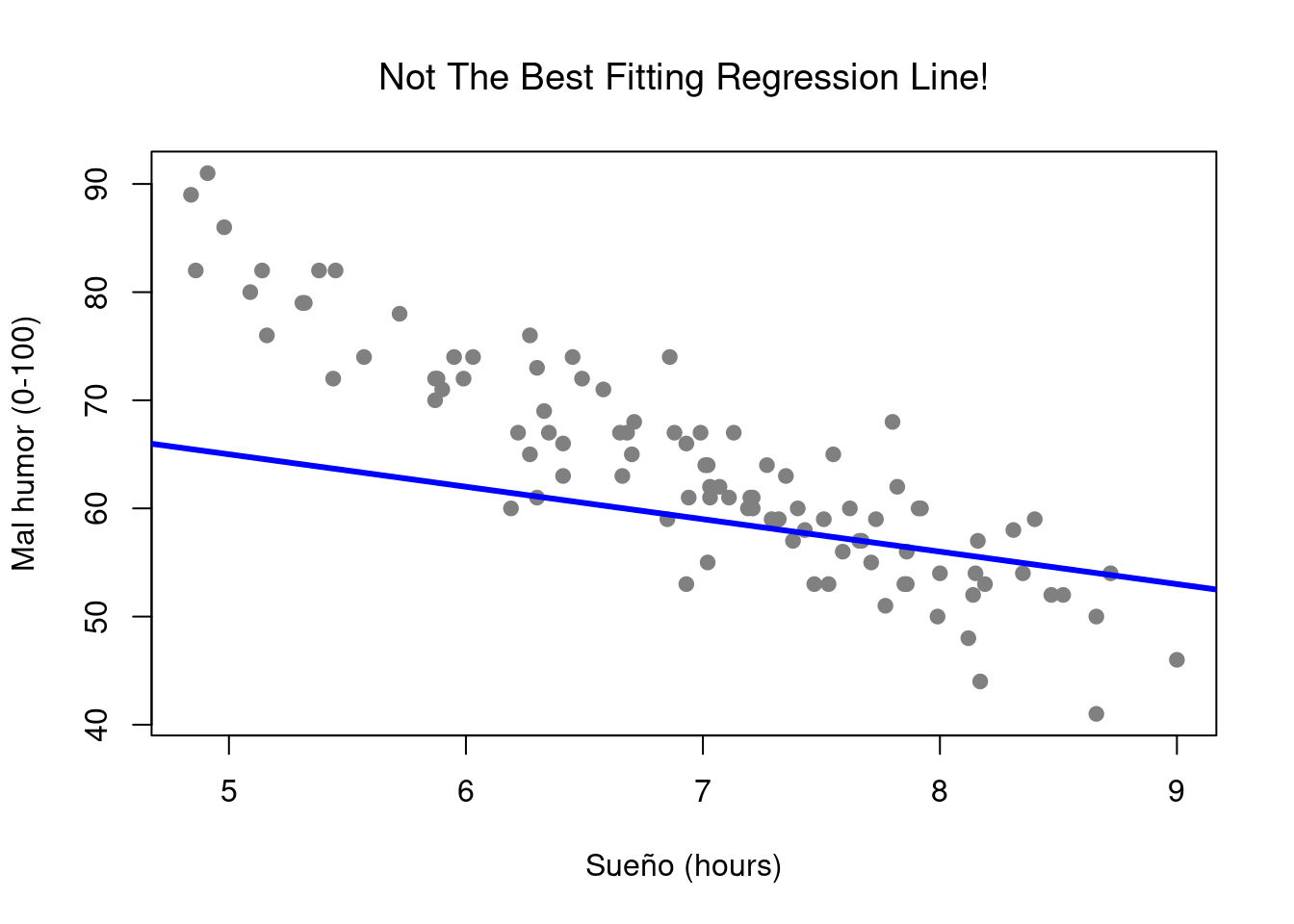
Figura 5.3: Por el contrario, este gráfico muestra los mismos datos, pero con una elección muy pobre de la línea de regresión dibujada en la parte superior.

El diagrama de dispersión real que dibujamos es el que se muestra en la Figura @ref(fig: regression0), y como vimos anteriormente, esto corresponde a una correlación de \(r=-.90\), pero lo que nos encontramos imaginando en secreto es algo que se ve más cerca de la Figura  (???) (fig: regression1a). Es decir, dibujamos mentalmente una línea recta a través del medio de los datos. En estadística, esta línea que estamos dibujando se llama línea de regresión. Tened en cuenta que la línea de regresión pasa por el centro de los datos. No hay nada parecido en la gráfica que se muestra en la Figura @ref(fig: regression1b). La línea dibujada en la Figura 5.3 no “se ajusta” muy bien a los datos, por lo que no tiene mucho sentido proponela como una forma de resumir los datos, ¿verdad? Esta es una observación muy simple de hacer, pero resulta ser muy poderosa.

La fórmula para una línea recta generalmente se escribe así: \[ y = mx + c \] Las dos variables son \(x\) y \(y\), y tenemos dos coeficientes, \(m\) y \(c\). El coeficiente \(m\) representa la pendiente de la línea y el coeficiente \(c\) representa la intersección \(y\) de la línea. Profundizando, la intersección se interpreta como “el valor de \(y\) que obtienes cuando \(x=0\)”. De manera similar, una pendiente de \(m\) significa que si aumenta el valor \(x\) en 1 unidad, entonces el valor \(y\) aumenta en \(m\) unidades; una pendiente negativa significa que el valor \(y\) bajaría en lugar de subir.

Usamos exactamente la misma fórmula para describir una línea de regresión. Si \(Y\) es la variable de resultado (variable dependiente) y \(X\) es la variable predictora (variable independiente), entonces la fórmula que describe nuestra regresión se escribe así: \[ \hat{Y_i} = b_1 X_i + b_0 \]

Parece la misma fórmula, pero hay algunos detalles extra en esta versión. En primer lugar, observad que tenemos \(X_i\) y \(Y_i\) en lugar de simplemente los viejos \(X\) y \(Y\). Esto se debe a que queremos recordar que estamos tratando con datos reales. En esta ecuación, \(X_i\) es el valor de la variable predictora para la \(i\) ésima observación (es decir, el número de horas de sueño que obtuve el día \(i\) de este pequeño estudio), y \(Y_i\) es el correspondiente valor de la variable de resultado (es decir, el mal humor de ese día). Asumimos es que esta fórmula funciona para todas las observaciones en el conjunto de datos (es decir, para todos los \(i\)). En segundo lugar, observad se escribe \(\hat{Y}_i\) y no \(Y_i\). Esto se debe a que queremos hacer la distinción entre los datos reales \(Y_i\) y la estimación \(\hat{Y}_i\) (es decir, la predicción que hace nuestra línea de regresión). En tercer lugar, las letras utilizadas para describir los coeficientes de \(m\) y \(c\) cambian a \(b_1\) y \(b_0\). Esa es la forma en que a los estadísticos les gusta referirse a los coeficientes en un modelo de regresión. En cualquier caso, \(b_0\) siempre se refiere al término de intersección y \(b_1\) se refiere a la pendiente.

Independientemente de si estamos hablando de una línea de regresión buena o mala, los datos no encajan perfectamente en la línea. O, para decirlo de otra manera, los datos \(Y_i\) no son idénticos a las predicciones del modelo de regresión \(\hat{Y_i}\). Dado que a los estadísticos les encanta adjuntar letras, nombres y números a todo, hagamos referencia a la diferencia entre la predicción del modelo y ese punto de datos real como un residual o residuos, y lo denominaremos \(\epsilon_i\).⁵ Escritos usando matemáticas, los residuos se definen como:

\[ \epsilon_i = Y_i - \hat{Y}_i \]

lo que a su vez significa que podemos escribir el modelo de regresión lineal completo como:

\[ Y_i = b_1 X_i + b_0 + \epsilon_i \]

5.2 Estimación de un modelo de regresión lineal

Figura 5.4: Una descripción de los residuos asociados con la línea de regresión que mejor se ajusta

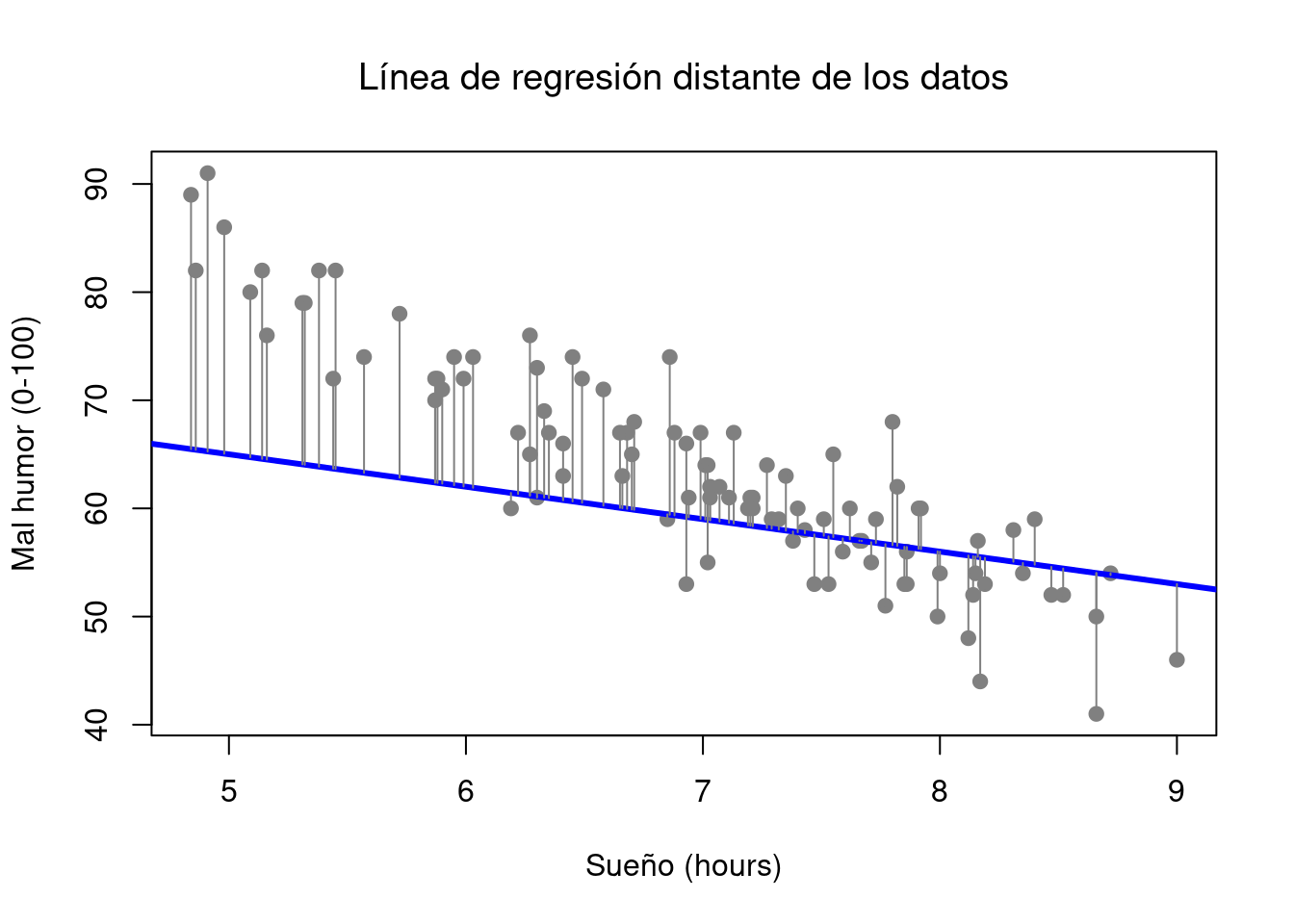
Figura 5.5: Los residuos asociados con una línea de regresión pobre

Bien, ahora redibujemos nuestras imágenes, pero esta vez agregaré algunas líneas para mostrar el tamaño del residual para todas las observaciones. Cuando la línea de regresión es buena, nuestros residuos (las longitudes de las líneas negras continuas) se ven bastante pequeños, como se muestra en la Figura 5.4, pero cuando la línea de regresión es mala, los residuos son un mucho más grandes, como puede ver al mirar la Figura 5.5. Lo que buscamos en un modelo de regresión son residuos pequeños. La línea de regresión de “mejor ajuste” es la que tiene los residuos más pequeños.

Los coeficientes de regresión estimados, \(\hat{b}_0\) y \(\hat{b}_1\) son los que minimizan la suma de los residuos al cuadrado, que podríamos escribir como \(\sum_i(Y_i-\hat{Y}_i)^2\) o como \(\sum_i{\epsilon_i}^2\).

Los coeficientes de regresión son estimaciones (estamos tratando de adivinar los parámetros que describen una población), razón por la cual hay unos pequeños sombreros sobre la fórmula, de modo que obtenemos \(\hat{b}_0\) y \(\hat{b}_1\) en lugar de \(b_0\) y \(b_1\). Finalmente, dado que en realidad hay más de una forma de estimar un modelo de regresión, el nombre más técnico para este proceso de estimación es regresión de mínimos cuadrados ordinarios (MCO).

En este punto, ahora tenemos una definición concreta de lo que cuenta como nuestra “mejor” elección de coeficientes de regresión, \(\hat{b}_0\) y \(\hat{b}_1\). Si los coeficientes de regresión óptimos son aquellos que minimizan los residuos de la suma al cuadrado, ¿cómo encontramos estos números? La respuesta real a esta pregunta es complicada y no le ayuda a entender la lógica de la regresión..⁶ R proporciona una manera más simple de calcular la regresión, utilizando la función lm () (abreviatura de “modelo lineal”).

5.2.1 Usando la función lm ()

La función lm() es bastante complicada: si escribe ?Lm, los archivos de ayuda revelarán que hay muchos argumentos que puede especificar. Sin embargo, en este momento, solo hay dos de ellos que nos interesan, y resulta que los hemos visto antes:

• fórmula. Una fórmula que especifica el modelo de regresión. Para los modelos de regresión lineal simple de los que hemos hablado hasta ahora, en los que tiene una única variable predictora, así como un término de intersección, esta fórmula tiene la forma resultado ~ predictor. Sin embargo, se permiten fórmulas más complicadas y las discutiremos más adelante.
• datos. El dataframe que contiene las variables.

La salida de la función lm() es un objeto bastante complicado, con bastante información técnica. Debido a que otras funciones utilizan esta información técnica, generalmente es una buena idea crear una variable que almacene los resultados de una regresión. Con esto en mente, para ejecutar la regresión lineal, hacemos:

regression.1 <- lm( formula = dan.grump ~ dan.sleep,  
                    data = parenthood )  

La fórmula utilizada es dan.grump ~ dan.sleep: en el modelo que estoy tratando de estimar,dan.grump es la variable resultado y dan.sleep es la variable predictora. De todos modos, lo que esto hace es crear un “objeto lm” (es decir, una variable cuya clase es "lm") llamada regression.1. Echemos un vistazo a lo que sucede cuando lo print():

print( regression.1 )

## 
## Call:
## lm(formula = dan.grump ~ dan.sleep, data = parenthood)
## 
## Coefficients:
## (Intercept)    dan.sleep  
##     125.956       -8.937

Hay dos piezas de información separadas. En primer lugar, R nos recuerda cuál fue el comando que usamos para especificar el modelo, lo que puede ser útil. Más importante desde nuestra perspectiva, sin embargo, es la segunda parte, en la que R nos da la intersección \(\hat{b}_0=125.96\) y la pendiente \(\hat{b}_1=-8.94\). En otras palabras, la línea de regresión que mejor se ajusta (ver la Figura 5.2 tiene esta fórmula:

\[ \hat{Y}_i = -8.94 \ X_i + 125.96 \]

5.2.2 Interpretación del modelo estimado

Lo más importante para poder entender es cómo interpretar estos coeficientes. Comencemos con \(\hat{b}_1\), la pendiente. Si recordamos la definición de la pendiente, un coeficiente de regresión de \(\hat{b}_1=-8.94\) significa que si aumento \(X_i\) en 1, entonces estoy disminuyendo \(Y_i\) en 8.94. Es decir, cada hora adicional de sueño que gano mejorará mi estado de ánimo, reduciendo mi mal humor en 8,94 puntos de mal humor. ¿Qué pasa con la intersección? Bueno, dado que \(\hat{b}_0\) corresponde al “valor esperado de \(Y_i\) cuando \(X_i\) es igual a 0”, es bastante sencillo. Implica que si duermo cero horas (\(X_i=0\)) entonces mi mal humor se saldrá de la escala, a un valor insano de (\(Y_i=125.96\)).

5.3 Regresión lineal múltiple

El modelo de regresión lineal simple que hemos discutido hasta este punto supone que hay una única variable predictora que le interesa, en este caso, dan.sleep. De hecho, hasta este punto, todas las herramientas estadísticas de las que hemos hablado han asumido que su análisis utiliza una variable predictora y una variable de resultado. Sin embargo, en muchos (quizás la mayoría) de los proyectos de investigación, en realidad tiene varios predictores que desea examinar. Si es así, sería bueno poder extender el marco de regresión lineal para poder incluir múltiples predictores.

La regresión múltiple es conceptualmente muy simple. Todo lo que hacemos es agregar más términos a nuestra ecuación de regresión. Supongamos que tenemos dos variables que nos interesan; tal vez queramos usar tanto dan.sleep comobaby.sleep para predecir la variable dan.grump. Como antes, dejamos que \(Y_i\) se refiera a mi mal humor el día \(i\)-th. Pero ahora tenemos dos variables \(X\): la primera corresponde a la cantidad de horas que dormí y la segunda que corresponde a la cantidad de horas que durmió un bebé. Así que dejaremos que \(X_{i1}\) se refiera a las horas que durmió Dan el día \(i\)-ésimo, y \(X_{i2}\) se refiere a las horas que durmió su bebé ese día. Si es así, entonces podemos escribir nuestro modelo de regresión así: \[ Y_i = b_2 X_{i2} + b_1 X_{i1} + b_0 + \epsilon_i \]

Como antes, \(\epsilon_i\) es el residuo asociado con la \(i\)-ésima observación, \(\epsilon_i={Y}_i-\hat{Y}_i\). En este modelo, ahora tenemos tres coeficientes que deben estimarse: \(b_0\) es la intersección, \(b_1\) es el coeficiente asociado con el sueño de Dan y \(b_2\) es el coeficiente asociado con el sueño de su hijo. Sin embargo, aunque ha cambiado el número de coeficientes que deben estimarse, la idea básica de cómo funciona la estimación no ha cambiado: los coeficientes estimados \(\hat{b}_0\), \(\hat{b}_1\) y \(\hat{b}_2\) son los que minimizan la suma de los residuos al cuadrado.

5.3.1 Haciéndolo en R

La regresión múltiple en R no es diferente de la regresión simple: todo lo que tenemos que hacer es especificar una “fórmula” más complicada cuando usamos la función “lm ()”. Por ejemplo, si queremos usar tanto dan.sleep comobaby.sleep como predictores en nuestro intento de explicar por qué estoy tan malhumorado, entonces la fórmula que necesitamos es la siguiente:

                    dan.grump ~ dan.sleep + baby.sleep

Observe que, al igual que la última vez, no he incluido explícitamente ninguna referencia al término de intersección en esta fórmula; sólo las dos variables predictoras y el resultado. Por defecto, la función lm () asume que el modelo debe incluir una intersección (aunque puede deshacerse de ella si lo desea). En cualquier caso, puedo crear un nuevo modelo de regresión, al que llamaré regression.2, usando el siguiente comando:

regression.2 <- lm( formula = dan.grump ~ dan.sleep + baby.sleep,  
                     data = parenthood )

Y al igual que la última vez, si print() este modelo de regresión, podemos ver cuáles son los coeficientes de regresión estimados:

print( regression.2 )

## 
## Call:
## lm(formula = dan.grump ~ dan.sleep + baby.sleep, data = parenthood)
## 
## Coefficients:
## (Intercept)    dan.sleep   baby.sleep  
##   125.96557     -8.95025      0.01052

El coeficiente asociado con dan.sleep es bastante grande, lo que sugiere que cada hora de sueño que pierde le pone mucho más gruñón. Sin embargo, el coeficiente de baby.sleep es muy pequeño, lo que sugiere que realmente no importa cuánto duerma su hijo. Para tener una idea de cómo se ve este modelo de regresión múltiple, la Figura @ref(fig:regresión múltiple) muestra un gráfico 3D que traza las tres variables, junto con el modelo de regresión en sí.

---

5. El símbolo \(\epsilon\) es la letra griega epsilon. Es tradicional usar \(\epsilon_i\) o \(e_i\) para denotar un residual.↩︎

6. O al menos, asumo que no ayuda a la mayoría de la gente. Pero en la remota posibilidad de que alguien que lea esto, ayudará a *saber eso la solución al problema de estimación resulta ser \(\hat{b}=(X^TX)^{-1}X^T y\), donde \(\hat{b}\) es un vector que contiene los coeficientes de regresión estimados, \(X\) es la “matriz de diseño” que contiene las variables predictoras (más una columna adicional que contiene todas unas; estrictamente \(X\) es una matriz de los regresores, pero aún no he discutido la distinción), y \(y\) es un vector que contiene la variable de resultado.↩︎